|
Abstract
Exact quantitative analytical
solutions of Einstein´s cosmological equations for a finite open (KOFL)
Universe and a finite flat (LCDM) Universe, result respectively infinite
total cosmic masses 
and 
very large but finite. The first value is
obtained with 
as given by 
(PLANCK, 2013) and 
(Gravitational Waves, 2017). This results in 
(dimensionless). On the other hand, the second
value is obtained with 
(Supernovae 2016) resulting in 
which excludes the possibility of an open 
Universe. In both cases 
(WMAP 2003 / PLANCK 2013) gives the time elapsed
between the Big Bang and today. According to Fr. Jaki (in full agreement with
Einstein and Lemaitre) the Universe must necessarily be finite on the
grounds of logical and metaphysical principles. Alan Guth and others have
proposed a flat Inflationary Universe which might be infinite and most
theoretical cosmologists today support a flat LCDM Universe and they do not
discard the possibility of an infinite self-sufficient Universe among many
multiverses.
1. Introduction
As noted recently by Julio A.
Gonzalo and Manuel Alfonseca rigorous cosmological work based upon Einstein´s
Cosmological Equations gives preference to the LCDM (Lambda Cold Dark Matter)
model based substantially in the Inflationary hypothesis of Alan Guth[1]. This model assumes zero space-time
curvature (
) and a non-zero cosmological constant (
). In addition to the cosmic density parameter 
, where 
is the critical mass density parameter
(dimensionless), another important dimensionless cosmic parameter is the
product 
dependent on the Hubble-Lemaitre ratio 
. As has been noted previously[2] the value of 
determined from the CBR (Cosmic Background
Radiation) is significantly different from that determined by Supernovae data2.
The value of 
, time elapsed since the Big Bang to today is very
accurately known from NASA’S WMAP satellite data and ESA’S PLANCK satellite
data which coincide within less than 1%. On the other hand, recent data on extracted from the collapse of two distant very
massive objects, agrees very well with the CBR value determined by PLANCK’S
data, but not with the Supernovae value, as shown below in Table I.
TABLE I
|
|
|
|
|
|
|
|
|
It is very important to note
that the compact rigorous[3]
solutions of Einstein´s Cosmological Equations for finite KOFL open
Universe (
) lead to
(1.1)
for y going from y
= 0 (Big Bang) to 
(very distant future), but that for a finite flat
Universe (
) the corresponding solutions of Einstein’s
Cosmological Equations lead to
(1.2)
for y going from y
= 0 (Big Bang) to (very distant future)
So 
is allowed to be 
for an Open Universe and 
would imply necessarily a Flat Universe.
This appears to be precluded by the 
value, in such a good agreement with the 
value.
It must be noted that the compact rigorous solutions of Einstein’s Cosmological Equations for a flat Universe lead to a finite mass for the Universe only slightly larger than the mass of the open Universe, evidently finite as assumed originally by Einstein and Lemaitre.
I the next section we will
examine quantitatively the case for a KOFL Open Universe
and for a LCDM Flat Universe 
, and we will make finally the pertinent concluding
remarks, having into account Fr. Jaki’s view on the subject.
2. The case of an Open Universe
Einstein´s cosmological Equations can be summarized3 by
(2.1)
where R is the cosmic
radius, 
its time derivative, G Newton´s
gravitational constant
,
the mass density (including matter mass and
radiation mass), k the space-time curvature, c the speed of light
in vacuum 
, and 
the so called
Einstein’s cosmological constant.
In principle k could be
k < 0, k = 0, and k > 0. The case of k > 0
(closed universe) may be excluded from further consideration because it
requires that 
, contrary to the observational evidence.
For an open (k < 0)
Universe assuming 
, something which Einstein did regret not to have done
after examining the available observational evidence Eq. (2.1) becomes
(2.2)
We can define
(2.3)
and integrate the nonlinear differential equation3 resulting on
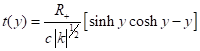(2.4)
(2.5)
From Eq. (2.4) and Eq. (2.5) we can get directly, having into account that
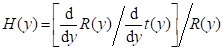, the dimensionless product
(2.6)
which allows us to get 
knowing[4]
, and 
, resulting in
(2.7)
Then
we get 
from Eq.
(2.4) knowing, as we know, resulting in
(2.8)
Having into account that
(2.9)
and that at 
we have 
we get
and therefore that
(2.10)
This implies that
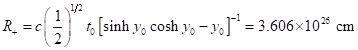(2.11)
and
(2.12)
The density parameter 
, where 
and 
, which comes out to be 
, the redshift 
, and the cosmic background temperature 
after decupling, which is fixed[5] accurately using NASA’S COBE satellite
data
.
Table II below gives the evolution of cosmic quantities as we
go back in time from the present (z = 0) to protogalaxy formation[6] (z 
10) to the time at which
Table II
|
y |
t (s)
|
H (s-1) |
Ht |
|
R (cm) |
|
z |
T (ºK) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Knowing 
and 
it is possible to determine the total mass of
the open universe () as
(2.13)
which, of course, is very
large but finite. This value is reasonable, since we know that there are
about 1011 galaxies each with about 1011 stars in the
universe. The average mass of a typical star would be then about 1032 g,
not far from the mass of the sun, 
.
3. The case of a Flat Universe with Λ > 0
In this case Einstein’s
Cosmological Equations reduce to
(3.1)
which has compact solutions2
given by
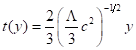(3.2)
(3.3)
From Eq. (3.2) and Eq. (3.3)
we get the pertinent dimensionless product
(3.4)
and using now 
, and again 
, we get
(3.5)
Then we can get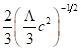 
from Eq. (3.2) for 
, resulting in
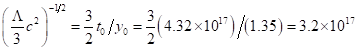(3.6)
which implies 
, and taking into account that for 
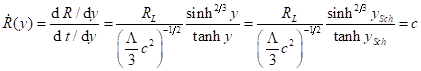(3.7)
where 
, we finally get
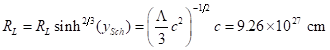(3.8)
The present radius of this
flat universe is then
(3.9)
The density parameter is again
, the redshift is , and the cosmic background temperature is again 
, after decoupling, with 
.
Table III gives the evolution of cosmic quantities going back
form the present (z = 0), but, since zSch = 0.5341 is less
than 
for protogalaxy formation, no room for such
formation is allowed in a LCDM flat Universe according to the previous
analysis. Decoupling (atom formation) takes place in a flat universe at a
temperature close to 2000 ºK.
Table III
|
y |
t (s)
|
H (s-1) |
Ht |
|
R (cm) |
|
z |
T (K) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The total mass of the flat
universe 
can be determined from
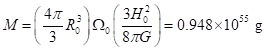(3.10)
which is not very dissimilar to M for an open universe as given by Eq. (2.12), and if very large, but finite.
4. Concluding remarks
Finally let us say that the most accurate observational values of t0 and H0 as given by the CBR and Gravitational Waves favour finite Open Universe with F while Ho from Supernova favour a finite Flat Universe with k = 0 F which implies a maximum redshift Zm = 0,534 < Z pg (observed from protogalactic quasars) = 10.
We can conclude with an extensive quotation of Fr. Jaki at the end of his “Postscript” to the 2nd ed. ff “God and the cosmologists”[7]:
“It therefore remains largely a matter of intellectual courage to stand up for the validity of the ontological sense of the question, “why such and not something else?” as it is posed by any finite (underlined by JAG) thing, be that thing the Universe itself. It takes even greater courage, although it should seem a mere matter of logic, to vindicate the mind`s rights to a truly satisfactory answer posed by any finite existent, which the Universe certainly is. The Universe if finite at least in the sense of being restricted to a very narrow set of parameters. Not all that is conceivable does exist. Curiosity about this fact in the ontological sense is what evokes God, the Ultimate being in intelligibility, anywhere but especially within the framework of cosmology or the study of the Universe, which is supposed to be the All, a coherent Totality. Devotees of incoherence have not legitimate place in science, let alone in the science of cosmology as long as –logy is tied to logic, and the latter to logos, and cosmos stands for a coherent all and not for a scientific fad. The All is the Universe, writ large. Not being necessarily what it is, such Universe remains a stubbornly vivid pointer to God. He is the only explanation why the All is not a glorified chaos but a cosmos which cosmologists, though they cannot create anything by any stretch of imagination, are specially privileged to investigate”.
March 1998 S.L.I.
We have seen in this work presented here to commemorate the 10th anniversary of Fr. Jaki´s death that, from a rigorous astrophysical perspective, the data obtained by first class contemporary experimentalist measuring gravitons ejected by a distant colliding pair of Newton star support a value for the Hubble-Lemaitre parameter consistent with a finite Universe in agreement with as well as with no others than Einstein and Lemaitre, as well as with Fr. Jaki.
[1] Alan Guth, “The Inflationary Universe” (Perseus Books: Cambridge Massachusetts, 1977).
[2] See f.i. Julio A. Gonzalo, “Cosmic Paradoxes” 2nd ed. (World Sci.: Singapore 2017) and references there in.
[3] Julio A. Gonzalo, Ibídem Chap. 11, pp. 9-76.
[4] See f.i.D. Holz, S. Hughes and B. Schutz, “Physics Today” December 2018, Vo. 71, num. 12 pp 34-40 and references therein.
[5] Julio A. Gonzalo, “The Intelligible Universe: An Overview of the Last Thirteen Billion Years” (Word Sci.: Singapore, 2008) and references therein.
[6] Joseph Silk, “The Big bang”, 3rd. ed. (W. H. Freeman and Company: New York 2001) and references therein.
[7] S.L. Jaki, “God and the Cosmologists” (Real View Books: P.O. Box 1793, Fraser, Michigan, 48048) p. 271.
A Note on Membership in the BWW Society-Institute for Positive Global Solutions: Standard Membership requires an academic level of at least Associate Professor (or the equivalent in non-academic fields); Fellowship Status is reserved for Full Professors or equivalent.