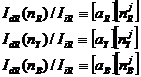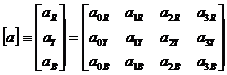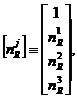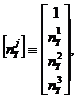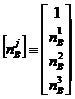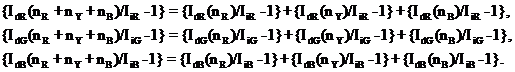Fundamentals and Practices of Sensing Technologies

by Dr. Keiji Taniguchi, Hon. Professor of Engineering

University of Fukui, Fukui, Japan

Xi’ an University of Technology, Xi’ an, China

Dr. Masahiro Ueda, Honorary Professor, Faculty of Education and Regional Studies

 University of Fukui, Fukui, Japan

Dr. Ningfeng Zeng, an Engineer of Sysmex Corporation

(A Global Medical Instrument Corporation), Kobe, Japan

Dr. Kazuhiko Ishikawa, Assistant Professor

Faculty of Education and Regional Studies, University of Fukui, Fukui, Japan

 

[Editor’s Note: This paper is presented as Part IX of a series from the new book “Fundamentals and Practices of Sensing Technologies”; subsequent chapters will be featured in upcoming issues of this Journal.]

 

 

Chapter Five – Part I

 

Abstract for Chapter 5

 

In chapter 4, we have described same applications of measurement technologies by means of laser attenuation to manufacturing plant. In this chapter, same applications of measurement technologies by means of laser reflection were described. That is, a color sensor for dispersive dye is described in 5.1, a counter sensor for cloth weft in 5.2, a vibration sensor for speaker surface in 5.3, a torsion sensor in power transmission shaft in 5.4, a diameter sensor for polyethylene filament in 5.5, a displacement and vibration sensor for the pipe in 5.6, a cross-linking sensor for enamel on a copper wire in 5.7, a surface creases sensor for polyethylene sheets in 5.8, a surface displacement sensor in 5.9, a hybrid sensor for the surface displacement in 5.10, a thickness sensor for glass bottle in 5.11, and a thickness sensor for film in 5.12.

 

5.1 Color Sensor for Dispersive Dye

 

5.1.1 Introduction

 

We have previously reported on the real-time optical measuring method¹⁾ and the monitoring system²⁾ for dye color and concentration for ionic dye, i.e., water-soluble dye. In this case, a light attenuation method can be effectively applied since the light intensity passing through the dye decreases exponentially as dye concentration increases up to a range of practical concentration.

On the contrary, the light intensity decreases within an extremely small concentration range for a dispersive dye, i.e., an oil dye which is mainly used for a synthetic fiber. It is, therefore, necessary to dilute dye of practical concentration to a reasonable concentration. This gives up a real-time detection which is indispensable in a dyeing process. Our new method enables real-time detection.

The oil dye has roughly a spherical shape and is suspended in water with hydrophobia agent. It is then considered that the light intensity scattered on the dye sphere increases as the dye concentration increases. That is, the scattered light intensity may be applied for the measurement of the oil dye concentration. We call this " the light scattered method".

In this section, the principle and the experimental result of the light scattered method are described, and the flexibility of the sensor is discussed from the viewpoint of practical use.

 

5.1.2 Principle and Method

 

The mathematical principle of the method is the same as used previousy.²⁾ That is, three unknown parameters, i.e., each concentration of three base color dyes, can be determined by solving a simultaneous cubic equations with three unknowns-but the method is physically quite different from the previous one, i.e., the scattered light intensity is used for three known parameters in this case. A transmitted light intensity was used for the known parameters in the previous method and an exponential function can be applied between incident and transmitted light intensities for ionic dye. Tailor expansions, however, must be used for oil dye since part of the relations is complicated, the reason of which will be discussed in section 3. Thus, the method is, mathematically, applicable for popular use.

Fig. 5.1 shows the principle of the method. Laser light containing the three base colors (red, _R; green, _G; blue, _B) is guided into a measuring cell, in which three base colors of oil dye (red, C_R; yellow, C_Y; blue, C_B) are suspended. The oil dye scatters light on the surface.

 

 

 

 

 

Fig. 5.1  Optical principle of the method. Part of the incident light of three base colors is scattered from an oil dye consisting of the three base dye colors.

 

 

The scattered light intensity, I_d, is expressed by a Tailor expansion as follows:

 

(5.1)

 

where I_i shows the incident intensity of the laser light, n the concentration of the oil dye and K_i(i=0,1,2,3,...) the scattering coefficient in a broad sense. In particular, K₀ shows the scattered light intensity from a glass plate and pure water without dye. It is obvious from a physical point of view that I_d increases linearly with increasing dye concentration, n, if it is reasonably diluted. However, the relation between scattered light intensity and the dye concentration is not so simple in practice, as shown later (Fig. 5.4(b)). It depends not only on the dye concentration but also on a combination of dye color and wavelength of the laser light.

The basic relation between scattered light intensity I_d and dye concentration n(n_R,n_Y,n_B) is concretely expressed as follows:

 

(5.2)

 

Where I_iR and I_dR show an incident and a scattered laser light intensities of wavelength _R, j= 0,1,2 and 3, and the matrices [a]and[n^j]are expressed as follows:

 

 

Where [a] shows a scattered coefficient in a broad sense, as shown in Eq. (5.1). The same relations are given for the laser light of wavelength _G by replacing [a] with [b], and I_dR and I_iR with I_dG and I_iG, and ,also, for the laser light of wavelength _B by replacing [a] with[c], and I_dR and I_iR with I_dB and I_iB. These 36 scattering coefficients were determined by the method of least squares from nine relations between scattered light intensity and dye concentration obtained experimentally.

The scattered light intensity from mixed dye may be superposed of each light intensity from three color dyes. This is indispensable to our method and is realized within a reasonable range of dye concentration, as shown in Fig. 5.3. That is, the expressions for this superposition principle can be shown as follows;

 

(5.3)

 

The left-hand terms in these equations are the total light intensities from the oil dye mixed with three base colors and then the known quantities. On the right-hand side, the unknown quantities, i.e., the dye concentrations n(n_R, n_Y, n_B), are contained in the form of Eq.(5.2). The equation can be solved by the Levenberg-Marquardt-Morrison's method.³⁾

Figure 5.2 shows the system for the measurement. A semiconductor laser was used for red light of wavelength _R=670 nm and a multiline Ar ion laser was used for green and blue lights of wavelengths _G=515 nm and _B=458 nm, respectively. The output intensity of the laser light scattered from the oil dye filled in the cell was measured on a photodiode and converted to an electric signal. The signal was amplified, sampled and digitized in 12 bits. The maximum sampling frequency of the data acquisition was limited to about 1 kHz by the A/D converter. The digitized signal was used to obtain the relations between the scattered laser light intensity and the dye concentration. The 36 scattering coefficients were obtained by the method of least squares from these relations and were used in Eq. (5.3) to calculate the concentration. The results were displayed on the monitor. All the data in this calculation were obtained by averaging 80 samples.

 

 

 

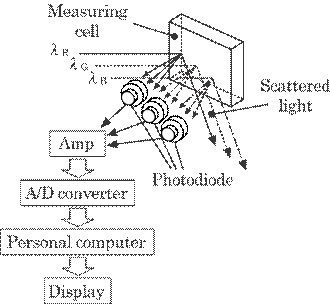
Fig. 5.2 Optics and sensor system.

 

 

5.1.3 Experimental Results and Discussions

 

We performed first of all, an experiment to confirm the superposition principle. Figure 5.3 shows the result. As is shown, the scattered light intensity from the mixed oil dye almost equals the sum of light intensities from each color of dye. The relation, however, can be realized only in the limited range of concentration up to about 0.01 g/l. The concentration of 0.01 g/l is slightly insufficient for a practical dye concentration used in dye process. This is the only one weak point of our method. The actual sensitivity of the method depends on this accuracy of the superposition principle. However, the small change of dye concentration in the neighborhood of practically used concentration may be detected with high sensitivity by this method, which is discussed bellow. This seems to be most important in practical use.

 

 

 

 

 

 

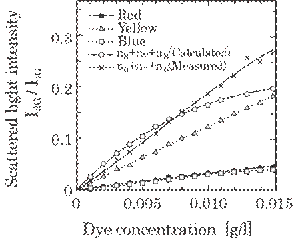
Fig. 5.3 Scattered light (wavelength of 670 nm) intensity from each color of dye concentration and the one for mixed dye concentration with a theoretical intensity.

 

 

Figures 5.4(a) and (b) show examples of the relation between scattered light intensity and dye concentration. Figure 5.4(a) shows an example of a simple relation and 5.4(b) a relatively

 

 

 

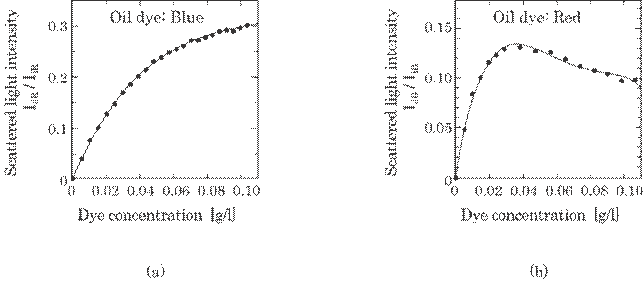
Fig. 5.4 Scattered light intensity for dye concentration: (a) for laser light of wavelength _R=670 nm and for blue dye; (b) _B=458 nm and red dye.

 

 

complicated one. In figure 5.4(a), it is naturally considered, in the diluted dye, that the scattered light intensity increases linearly as the number of dye particles in the unit volume increases, i.e., dye concentration, n. The light intensity, however, may become proportional to n^2/3 since the scattered light from inner area cannot pass through the dye cell to the photodiode due to a screening effect of the outer particles, and then the effective scattered light into the photodiode results from only an extremely thin layer of the surface. In figure 5.4(b), on the contrary, the complexity may be caused by the scattering and absorption of laser light on the dye particle. However, it can easily be fitted to the experimental results with high accuracy by using a Taylor expansion up to n³ terms. The other relations were obtained for all combinations of the three base colors of dye and laser light. All the scattering coefficients were obtained from these nine relations between scattered light intensity and dye concentration by the least squares method.

Table 5.1 shows all the coefficients. The coefficients independent of the dye concentration, i.e., a₀, b₀ and c₀, have to be one essentially, as seen in Eq. (5.1) and almost equal to one practically as shown in this table.

 

Table 5.1 Scattering coefficients obtained from the relation between the scattered light intensity and the dye concentration by the least squares method for all combinations of light colors and dye colors.

 

 

 

 

The experiment of increasing each color dye successively was carried out to confirm the reliability of the method. The dye concentration in the cell filled with pure water was increased successively by the droplets of high concentration dye. Figure 5.5(a) and (b) show examples of the calculated concentration from Eq. (5.3) and the theoretical one for blue and red dye, respectively. The experimental sensitivity is restricted to the error between calculated and theoretical concentrations. It can be seen that the experimental sensitivity is about 1 mg/l, which is sufficient for practical use.

 

 

 

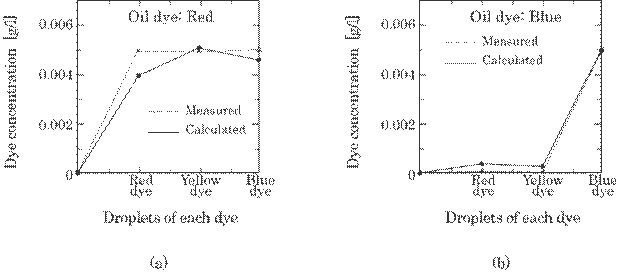
Fig. 5.5 Calculated dye concentration and the real one, i.e., theoretical concentration, for the droplets of each dye into the water: (a) for red dye; (b) for blue dye.

 

 

As discussed above, the reliability of this method is based on the fact that the superposition principle is realized. The concentration range of high accuracy is between 0 and 20 mg/l, which is inadequate in practical use. However, the small change of dye concentration n around the practically used concentration n₀ due to the small change of scattered light intensity I_d can be calculated by using the differential coefficient of the graphs in Fig. 5.3, (I_d)'_n=n0. Since the relation between scattered light intensity I_d and the dye concentration n can be expressed as in Eq. (5.2), n can be expressed as follows,

 

(5.4)

 

In this sense, Fig. 5.5 shows the results around n=0.

 

In conclusions, the following results were obtained.

 

(1)  The method is based on the principle of light scatter and is then applicable for dispersive dyes and so on.

(2)  The sensitivity of the method was about 1 mg/l and may be satisfactory for dyeing machines presently on the market.

(3)  The system can then be effectively used for monitoring or detecting a small change of dye concentration.

 

5.2 Counter Sensor for Cloth Weft

 

5.2.1 Introduction

 

In the textile industry, two major parameters are left to be studied in the production process, the cloth length and the cloth weft density which is given by a weft numbers per unit length. The former is the business basis between a seller and a buyer, and the latter determines aspect of the cloth, soft or rough. The length of the cloth changes with the tension and the history after weaving such as the stored time and the stored condition. Those two parameters can be precisely determined by counting the weft number and measuring the cloth length simultaneously. Since the weft density is given in the weaving process, the cloth length can be determined by measuring the weft number.

The purpose of this study is to improve the previously reported system⁴⁾ for an industrial use. The present system provides a good accuracy and a high counting speed enough for various types of knitting machines.

 

5.2.2 Method and System⁵⁾

 

We have proposed the light attenuation method⁴⁾ for counting cloth weft number by means of light passed through the cloth. In this system, a light source and a light receiver were set up on the opposite side of the cloth. Then, this method can be effectively used only when the cloth is thin and light passes through the cloth with a little attenuation.

On the contrary, the principle of the present method is based on the light scattering on the cloth. The method can then be applied to a thick cloth such as a light shielding curtain as well as a thin cloth. Further, it can be also applied to the cloth of a different Moire appearance of head and tail, to which the light attenuation method cannot be applied. The light scattering method can, thus, be widely applied. The method, further, has an advantage over the light attenuation method from a practical point of view, that the sensor head including both light source and light receiver can be incorporated in a body since they are set up on a same side to the cloth.

Fig. 5.6 shows a sensor head (a) and a whole system (b) of the method. A sheet-like laser light illuminates the cloth with parallel to a Moire appearance of the cloth as shown in Fig. 5.6(a). The scattered laser light is received by a PIN photodiode. A difference in direction between the sheet-like laser light and the Moire appearance line(for short "Moire line") may cause a complicated wave form of the received intensity and then yield a count error of the Moire line number. This will be discussed in 5.2.4. The output signal of the photodiode is then led into a counter system consists of an amplifier, digitizer(called V detector) and counter. The V detector reforms sine-like wave form to a square waves. The Moire line can then be

 

 

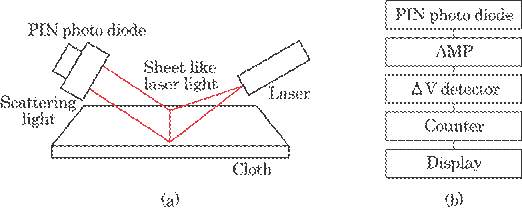
Fig. 5.6  Experimental system. (a) Sensor head and (b) Signal processing system.

 

 

exactly countered and then expressed on the display. Thus, the method in this paper is fundamentally to count the Moire lines. The sine-like wave results only from the Moire appearance of the cloth surface and does not depend on the speed of cloth motion. This may be one of the merits over other methods.

The weft density and the Moire density are usually different. There is, however, a definite relation between them depending on the weaving manners, such as plain weave, twill weave and sateen weave. We can then determine the weft number from the Moire line number.

 

5.2.3 Experimental Results⁵⁾

 

Figure 5.7 shows representative examples of the clothes having various Moire appearance. This Moire appearance results from the strength of the scattered light intensity due to an uneven cloth surface and yields sine-like wave for the output signal on the PIN photodiode. In each of the photograph, the left-hand side photographs show the head of the cloth and the right-hand side the tail. The black points at the bottom in each photograph show a measurement for 1 mm length. The Moire appearances of the head and tail in each cloth are quite different as shown in this figure except for (a). These clothes are all knitted together with thick thread bundled by some fine threads. The thick lines in each figure show the laser light cross-sections irradiated on the cloth. The line must be parallel to the Moire line, as much as we can, to obtain sine-like wave intensity. This enables us count the Moire line numbers accurately. A slight difference in directions between both lines may lead to a miscount of the Moire line numbers as discussed in 5.2.4.

 

 

 

 

Fig.5.7 Photographs of the cloth samples. Left shows the head and the right the tail. (a) Examples of plane weave, (b) twill weave, (c) sateen weave, and (d) a towel.

 

 

Fig. 5.8 shows the output signals of the scattered light intensity received by PIN photodiode(upper side) and the square waves reformed by V detector(lower side). We have examined for ten kinds of clothes and found out that the count error rate was below 1% for all clothes with a few marked exceptions which have not a clear Moire appearance such as in Fig. 5.7(d). We are now under study in this problem.　

We have further examined the system for the industrial use. The system was set up in a manufacturing plant. Table 5.2 shows an example. The error between mean value and number of Moire lines per unit length was found to be less than 1% in each measurement. The speed of the cloth movement was 75m/min. The cloth used was the one described in Fig. 5.7(b).

 

 

 

 

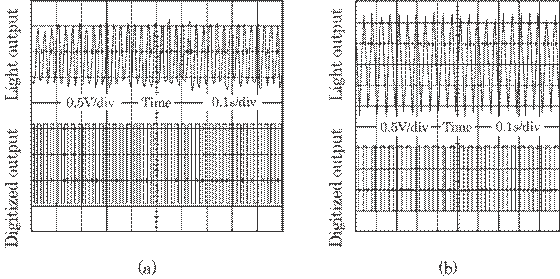
Fig.5.8 Wave form of the scattered laser light intensity at the PIN photodiode (upper side) and the square waves reformed by V detector (lower side). (a) and (b) correspond to the experimental results of (a) and (b) in Fig. 5.7. These results were obtained where sheet-like laser is parallel to the cloth Moire line as shown 1 in Fig. 5.9 (a).

 

 

Table 5.2 Measured numbers of cloth Moire line in industrial use and count error rate from the mean value (Cloth speed: 75m/min).

 

 

 

The maximum counting frequency was found to be above a few tens kHz in the best condition without interpolation method discussed in section 5.2.4. It is limited by a processing speed of the computer to interpolate a complicated wave-form to a sine-like wave-form. Even in this case, it can be above 10 kHz.

 

5.2.4 Discussions

 

A. Improvement of the Accuracy

 

The accuracy of counting depends basically on the degree of the parallel between both line directions of the sheet-like laser light on the cloth and of the Moire appearance. Figure 5.9 shows a schematic diagram of this relation. The cross-section of the sheet like laser light of width, w, and length, l, illuminates the cloth of Moire line pitch p, where three cases 1,2 and 3 are shown as the examples. It was found from the experiment that the high contrast sine-like wave can be obtained when the width is between 1/2 and 1/3 of the Moire line pitch, p, and the length is between 5 and 20 times of the width.

 

 

 

Fig. 5.9 A relation between directions of the sheet-like laser light and the Moire line. 1 is a case of perfect parallelism, 2 a slight lack of parallelism and 3 a lack of parallelism.

 

 

Fig. 5.10 shows similar waves to Fig. 5.8, which corresponds to the cross section of sheet-like laser light in Fig. 5.9 (2). They are complicated in particular Fig. 5.10(b) as compared to Fig. 5.8. An amplitude decrease of the sine-like waves may be due to a slight decrease of parallelism between both lines as shown in Fig. 5.9 (2) and (3). The slight decrease of parallelism is unavoidable in an industrial application because of a twist of the Moire appearance caused by an unbalanced tension of the cloth. It does not, however, cause a miscount since a correct square waves are obtained as shown in Fig. 5.10(a). On the contrary, a large distortion of the sine-like waves due to a lack of parallelism may cause a miscount as shown in Fig. 5.10(b). But the lack of parallelism was found to be rather small in the experiment at the manufacturing plant as shown in table 5.2. The distortion may, rather, be due to the lack of contrast of the Moire appearance.

The problem of the degree of parallelism may be easily solved by the use of the sheet-like laser light with a short length. It was, however, found from the experiment that the contrast of the scattered light intensity was also decreased. Thus, it is essential to find a point of compromise between the length l and the pitch p. This is, however, not an essential solution.

Three essential methods may be considered to solve this problem. The first is to reform the complicated wave form to a sine-like wave by the interpolation method. This can be done by a software technique and may be simplest and effective method from a practical point of view. The second is to use two PIN photodiodes placed at different position. In this case, one photodiode may, at least, receive a right sine-like wave even if the other receives a complicated wave. The count is always done by a right sine-like wave using a OR-logic circuit.

 

 

 

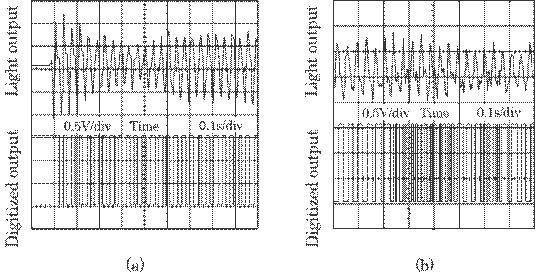
Fig. 5.10 Wave form of the scattered laser light intensity and corresponding square wave form for the cloth in Fig. 2(c). (a) shows a case where sheet-like laser is slightly inclined to Moire line as shown 2 in Fig. 4 and (b) rather inclined to Moire line as shown 3 in Fig. 4.

 

 

 

Thus, even if each photodiode has a count error rate of 5%, both photodiodes may reduce a count error rate to 0.25%(=0.05*0.05). The third is to adjust the laser light direction parallel to the Moire line of the cloth by means of feedback system, where a signal of a phase difference of the light intensity received on both photodiodes is used to rotate slightly the direction of the laser mounted on a rotary machine.

 

B. System for Industrial Use

 

The sensor head is usually fixed at a position and the cloth moves in an industrial use. It has, however, to be moved when the cloth is at rest. Figure 5.11 is a proposed system acceptable for these two purposes. The laser mounted on the belt is moved at a constant speed by a motor drive when the cloth is at rest and is fixed at a proper position when the cloth is moved. The laser and the PIN photodiode are confined in a light shielding box to eliminate the back ground light noise.

 

 

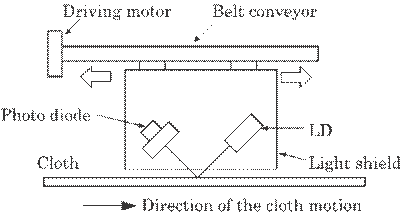
Fig. 5.11 Proposed counter system for cloth weft number using laser light for industrial use.

 

 

In conclusions, the following results were obtained.

 

(1) This system can be applied to various kinds of clothes.

(2) It can be applied to both cases, i.e., cloth is at rest and moved.

(3) It's accuracy is above 99%.

(4) It has a counting frequency of above 10 kHz.

 

5.3 Vibration Sensor for Speaker Surface

 

5.3.1 Introduction

 

A sound speaker for a high frequency of approximately 10 kHz is usually composed of thin mirror-like metal plates. The efficiency of the speaker will be determined by the material, thickness, and tension of the metal. In practice, however, efficiency is determined by measuring the vibration amplitude due to an electric input power. Therefore, in order to evaluate the speaker quality, it is important and urgent to develop a practical method to measure the vibration of the micro-speaker with radius about 5 mm.

Generally, a vibration with amplitude above a few tens microns are measured by using a mechanical method.⁶⁾ Optical interferometry, in particular optical holography,⁷⁾ has been used to measure vibration with amplitude between 0.01 m and several microns. As to a vibration with amplitude about 10 m as that of our speaker, Doppler method is probably the only way to measure it. However, it is, in itself, a method to measure a velocity, and a particular improvement in optical arrangement and electronic circuit is necessary to use it as a detector for the vibration amplitude.⁸⁾ The system, therefore, is not simple and cost-effective for our case.

In this section, a simple method through measuring the multi-reflected laser beam "dispersion" due to vibration to measure vibration amplitude above 10 m is proposed.

 

5.3.2 Principle and Method

 

The basic idea of the proposed method is to use a plane mirror just on a vibrating speaker and to cast a multi-reflected laser beam between them on the detectors such as a screen and a CCD camera. The laser light reflected on the vibrating mirror disperses and becomes obscure slightly at the edge of the laser beam. Actually, the reflected laser beam is not dispersed but is deflected slightly from an original direction due to the vibration, but it seems dispersed, as the vibration frequency is so high as to detect it with eye and detector. We call the phenomenon "a dispersion" in this study. The dispersion increases linearly, according to the vibration amplitude; that is, the vibration amplitude can be detected by means of the dispersion. The dispersion is, however, usually very small. The multiple reflection increases the dispersion; that is, multiple reflection leads to high sensitivity of measurement.

A thin plate of the speaker will, actually, vibrate in such a fashion as circular arc shown in Figure 5.12. However, we decompose the circular arc into two linear planes; i.e., an inclined plane P₁ and a horizontal plane P₂, for a convenience of theoretical analysis. That is, an actual dispersion can be approximated by a combination of the dispersions on planes P₁ and P₂.

 

 

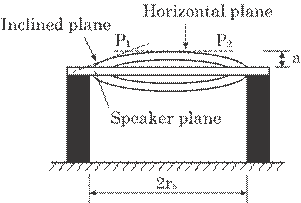
Fig. 5.12 Decomposition of practical vibration plane into two flat planes; i.e., an

        　inclined plane and a horizontal plane.

 

A. Laser Beam Dispersion on the Inclined Plane P₁

 

Figure 5.13 shows a comparison of the laser beam reflections between parallel plates and non-parallel plates. The laser beam reflected between non-parallel plates deflects from the one reflected between parallel plate. As was shown in a cut, when the mirror inclines slightly, , the reflected light deviates 2 from the original direction and this causes a dispersion of the laser beam. The mean inclination, <>, can be approximated by

 

(5.5)

 

where a is vibration amplitude at the central region and r_s is a radius of the speaker. The light deviates, finally, 2n<> after n times multi-reflection at a vibrating plane, as shown in Fig. 5.13(b). The dimension of the dispersion on the screen due to the vibration, W, will, then, be as follows at a distance R from the vibration plane to the screen.

 

(5.6)

Thus, the multiple reflection used in this method acts as an amplifier of the beam dispersion caused by the vibration amplitude. The amplification, i.e., the efficacy of multiple reflection, which is defined by W/W₀, can be given by

 

(5.7)

 

 

 

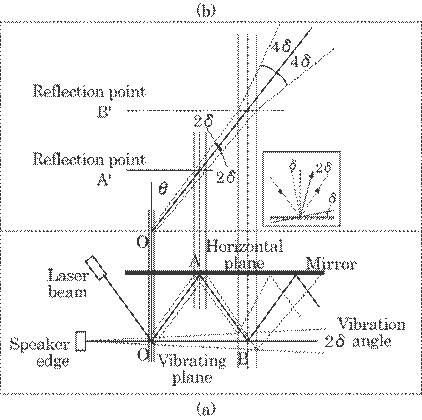
Fig. 5.13 Multiple reflections between parallel mirrors and non-parallel mirrors. (a)         Practical multiple reflections, and (b) laser beam profile symmetrical to a plane

mirror.

 

 

where W₀ is the beam spread represented by a single reflection, n=1. For example, we can obtain W = 2mm for a practical dimension of a = 10m, r_s = 5 mm, R = 100 mm, and n = 5. This value of W = 2mm can easily be observed by the naked eye. The actual inclination will be larger than the mean value given by Eq. (5.5) since the central zone of the speaker plane becomes horizontal. Thus, the actual spread dimension will be larger than W. This causes an error and will be discussed in section 5.3.3.

 

B. Laser Beam Dispersion on the Horizontal Plane P₂

 

In this case, in contrast to the case of the inclined plane, the laser beam does not diverge in itself in a free space since the direction of the laser beam does not deviate from that on the stationary plane. This renders the amplitude measurement difficult. However, application of multiple reflection can overcome this difficulty.

Figure 5.14 shows an illustration of the multiple reflection between the horizontally vibrating plane and the plane mirror. The reflection on the horizontally vibrating plane does not deflect the direction of the laser beam, but it rather increase the spread as shown in Figure 5.14(a). The spread of the laser beam at the vibrating plane, W', can be expressed as

 

(5.8)

 

 

 

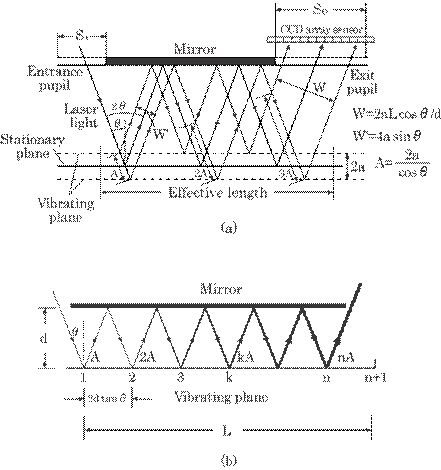
Fig. 5.14 Multiple reflections between a horizontally vibrating plane and a stationary           mirror. (a) Illustration of the beam spread. (b) Aspect of multiple reflections.

 

 

Thus, no spread exceeds 4a. The spread after a multiple reflection, however, can be larger than 4a. The spread after n times reflections can be calculated from a simple geometric consideration, as follows:

 

(5.9)

 

where L is an effective length of the vibrating plane mirror,  is an incident angle of the laser beam, and d is a distance between the vibrating plane and the mirror.

The amplification of the spread due to multiple reflection defined by W/W' is then

 

(5.10)

 

High amplification can, therefore, be obtained by using a large L, a small d, and a small . Remarkably small values for d would be impractical. We choose d = 0.5 mm, L = 2 mm, and = /18, for a = 10m with a practical speaker dimension of r_s = 5 mm. We then obtained W/W' = 11.34, and W = 78.8m, which may be measured easily by CCD camera.

Practical beam spread is a superposition of both the spreads expressed by Eqs. (5.6) and (5.9),

 

(5.11)

 

As discussed above, the dispersion on the inclined plane is rather large as compared with that on the horizontal plane for the speaker used in this study (dimension of r_s = 5 mm and mean vibration amplitude of a = 10m).

 

5.3.3 Experimental Results and Discussions

 

A preliminary experiment was conducted by using a large-scaled optical arrangement and by replacing the vibration amplitude with the static displacement of the mirror. That is, the displacement was considerably enlarged as compared with the practical dimensions for a convenience of measurement.

Figure 5.15 shows an example of a laser beam deflection on the inclined plane mirror. The

divergence of the laser beam increased linearly in accordance with the multiple reflection as predicted in section 5.3.2. Table 5.3 shows a laser beam spread on the horizontal plane mirror for some values of d and . The spread, W/W', also agreed well with the calculated values given by Eq. (5.10). From these results, the proposed method in this paper was found to be valid.

In this preliminary experiment, the laser beam from a He-Ne laser was used directly, but a laser beam with a small cross-section would be desirable in a practical use since a speaker plane is very small. This can be done easily by using the mirror with a small entrance pupil as shown in Figure 5.14(a). However, too small a pupil would cause a diffraction effect, which makes a detection of the beam spread difficult, and a proper beam size will be 500~1000 m.

 

 

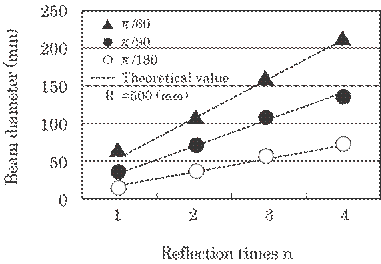
Fig. 5.15 The laser beam deflection on the inclined plane mirror.

 

 

Table 5.3 The laser beam spread on the horizontal plane mirror under the experimental

           condition of a = 1 mm and L = 100 mm.

 

 

 

 

Figure 5.16 shows an illustrative intensity profile of the laser beam on the observation plane. The broken curve represents the cross-sectional intensity of the laser beam itself, which is obtained by multiple reflection on a stationary mirror, and the solid curve represents the intensity profile obtained by multiple reflection on a vibrating plane. The intensity will, thus, fade around the edge region, W_p, due to the vibration, as discussed in sections 5.3.2. The value can be detected by using a CCD array sensor and a microscopic observation.

 

 

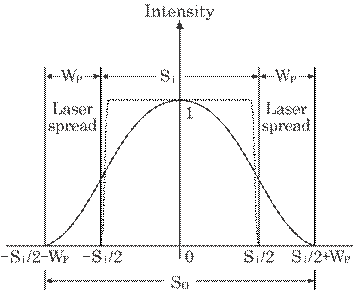
Fig. 5.16 An illustration of a light intensity profile on an observation plane. Broken           curve represents the intensity reflected on the stationary plane, and the           solid curve represents that on the vibrating plane.

 

 

In this preliminary experiment, the beam spread due to both inclined planes and parallel planes was detected separately. However, these spread are incorporated and cannot be detected separately in practice, as shown in Eq. (5.11). This causes a measuring error of this method. The considerable error factors of this method will result from a diffraction effect due to too small an entrance pupil, a laser beam divergence and a detection error. The first and the second factors will be eliminated since only a beam spread, W_p, due to vibration can be detected separately. Therefore, the remaining error factors will be the detection errors arising from a resolution of the detector and an indistinctness of the causes of the beam spread. The later error cannot be discussed theoretically; it can, only, be discussed experimentally. Only the former error factor will, then, be discussed in this paper. We can obtain the measuring errors for the vibration amplitude, a, from Eqs. (5.6) and (5.9), as follows:

 

and

(5.12)

 

Where W is a resolution of the detector. The measuring error on the inclined plane mirror is, then, a=(1/200)W for the previous values of r_s=5 mm, n=5 and R=100 mm, and that on the parallel mirror is a=(0.127)W for the previous values of d=0.5 mm, L=2 mm and =/18. The resolution of the CCD camera is usually a few microns and then the measuring error due to a resolution of the detector can be sub-microns.

 

In conclusions, the following results were obtained.

 

(1) This method uses multiple reflection between a vibrating plane and a plane mirror parallel to that vibrating plane, which is very simple.

(2) The measuring sensitivity of this method ranges between sub-microns and 1mm, which is sufficiently high for practical use.

 

5.4 Torsion Sensor in Power Transmission Shaft

 

5.4.1 Introduction

 

Metal shafts have long been used for the transmission of mechanical power. Examples include screw shafts and crank shafts in cars. Torsion is normally generated by a load since shafts are usually a few meters in length and a few cm in diameter.⁹⁾ Over time, shafts tend to break suddenly due to metal fatigue and overload. Such breakdowns will occasionally cause disastrous accidents. It is therefore desirable to monitor torsion in a rotating shaft in realtime.

In this section, we propose and verify a practical system to monitor torsion. The present method is based on laser reflection.

 

5.4.2 Principle and Method

 

We have previously proposed an optical method for detecting torsion in a power transmission shaft.¹⁰⁾ The basic principle of the present method is based on light reflection. Figure 5.17 shows the sensor head of the system. Two pairs of light sensors are used for this

 

 

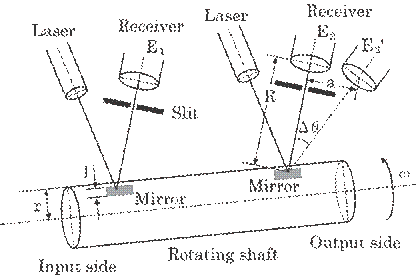
Fig. 5.17 Proposed sensor head for detecting torsion in a shaft.

 

 

purpose. One is attached to the input side of the shaft and the other to the output side. A load will cause torsion to occur between them. A pair of light sensors consists of a light source, mirror, slit, and light receiver. The light reflected on the mirror is captured by the receiver. A semiconductor laser is used as a light source and a silicon photodiode is used as a light receiver. The slit attached in front of the silicon photodiode is used to shield ambient light and obtain a square-like light signal. A curved mirror with the same curvature as the shaft is used, thus, both pulse signals are obtained simultaneously by the receivers when the laser illuminates the rotating mirrors. No time difference will exist between both signals when both mirrors are attached to the shaft in the same axial direction. A time difference t will, however, be produced due to torsion. The torsion angle  is in direct proportion to the time difference t as follows:

 

(5.13)

 

where  is the rotational frequency of the shaft. Thus,  can be detected by measuring t.

Figure 5.18 shows the principle of this method and Fig. 5.19 presents the system. Initially,

 

 

 

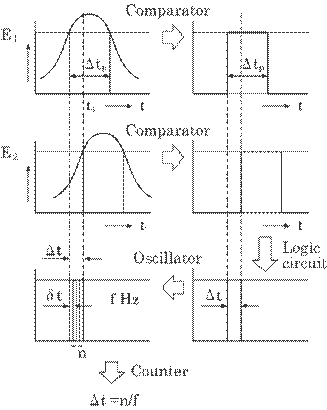
Fig.5.18 Method for measuring the torsion in realtime.

 

 

both received signals are transformed to square waves by a comparator. The time difference between them , t, can then be measured by a logic circuit and is finally digitized by an oscillator and a counter. The frequency of the oscillator, f Hz, determines the time resolution, i.e., measurable smallest amount of time t(=1/f). That is, the time difference is measured

by a relation, t = nt, where n is a pulse number within the time difference. The number

n can be detected by the counter. The torsion angle  can then be given by

(5.14)

 

 

 

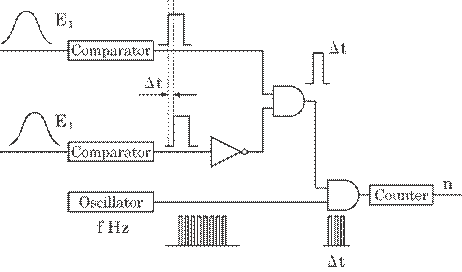
Fig.5.19 System for measuring the time difference digitally.

 

 

In order to measure the torsion accurately, the pulse number, n, in each time difference, t_i, was averaged over reasonable periods, T_a(=m2/), as shown in Fig. 5.20. The number m shows an integer that determines an interval for averaging. Each time difference at the sampling synchronized to the rotational frequency of the shaft has a different value, t_i(i=1~m), mainly due to the vibration of the shaft and the load. The pulse number thereby has a different value, n(n_i). In this paper, we denote the averaged values by < >, e.g., <t>, <n> and <>. The average has an effect on the estimated amount of torsion. This will be discussed further in section 5.4.4.

 

 

 

 

 

 

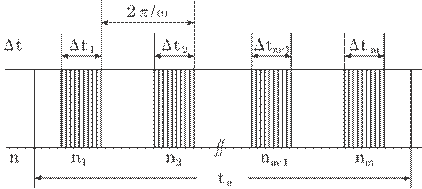
Fig. 5.20 Method for averaging.

 

 

5.4.3 Results

 

A preliminary experiment was conducted in order to verify the method. It is difficult to produce torsion experimentally. Torsion was simulated in the present study by a slight shift of the light receiver, E₂ to E₂', as shown in Fig. 5.17. The distance from the mirror to the receiver was R = 300 mm.

In the present experiment, there existed a small time difference between both light receivers, t₀, even in the absence of torsion, = 0. This was because of the optical arrangement of the light sources, the mirrors, and the light receivers. The net time difference, t, is then

 

(5.15)

 

where t_s represents the time difference, from when the torsion was simulated. An integer n₀ represents the pulse number withint₀ and n_s within t_s.

Table 5.4 presents a few examples of the pulse number for three different amounts of torsion. 20 samples were averaged, i.e., m = 20. The error rate of the pulse number from the mean value was within 5%. The accuracy of the torsion angle may then exceed 95% even without averaging. In this experiment, the rotational frequency was = 210 and the frequency of the oscillator was f = 1 MHz.

The net time difference t can then be obtained by Eq. (5.15), and the torsion amount  by Eq. (5.14). The shift amount of the light receiver, a, can easily be obtained by a relation <a>= R<>. Table 5.5 shows these values for three amounts of shift. It can be seen in table 5.5 that the measured torsion, a, agrees well with this method's calculated torsion <a>. Thus, the method used in this study was found to be valid.

 

 

Table 5.4 Pulse numbers within each time differencet_i(i=1~20) for three different amounts of simulated torsion.

 

 

 

Table 5.5 Calculated and measured torsions with pulse number and time difference.

          Experimental conditions: frequency of the oscillator, f = 1 MHz; rotational

          frequency of the shaft, = 210; distance from mirror to receiver, R = 300 mm.

 

 

 

5.4.4 Discussions

 

A. Accuracy

 

The error of the torsion depends on a fluctuation of n, f, and , as shown in Eq. (5.14). The values of n and  will continually fluctuate due to the load and the vibration of the shaft. The rotational frequency  will continually fluctuate due to a load. The fluctuation, however, has no effect on accuracy because both mirrors are attached to the same shaft. In addition, the high frequency oscillator does not fluctuate. Therefore, the only remaining possible error factor would be the fluctuation of n caused by a vibration of the shaft, n. The fluctuation i.e., error rate of the pulse number from the mean value, was a few percentages, which determines the accuracy of this method.

It is, however, possible to reduce the error to a negligibly small amount by averaging the measured values of n over a period of them, T_a(=m2/), as described in section 5.4.2, because the sum of n_i becomes zero. The data for the torsion can then be obtained at an interval of T_a. The interval T_a will usually be smaller than 1 s in practical use. The data can then be obtained in realtime. Thus, the method described in this paper will be free of error factors in principle.

 

B. Resolution of the Torsion Angle

 

The resolution of the torsion angle, i.e., detectable minimum torsion angle, is determined by /f, as expressed in Eq. (5.14). High resolution can thus be obtained with the high frequency of the oscillator. In this preliminary experiment, the resolution of the torsion angle, _min, can be calculated as _min = 210^-5 radian for f = 1MHz and = 210. The rotational frequency = 260 is usually used as power transmission. In this case, it becomes _min = 1.210^-4, which is more than sufficient for practical use.

 

C. Mirror Size

 

In order for the logic circuit to work effectively, the time difference t should be smaller than the pulse width t_p of the received signal, as shown in Fig. 5.18(a). This determines the mirror size l of the  direction, l = r_r, where r is a radius of the shaft (see Fig. 5.17). That is, the size _, should be larger than anticipated maximum torsion angle , _m. The value of _m = 110^-2 rad. will be more than sufficient for practical use. The minimum mirror size is therefore l = 0.4 mm for r = 40 mm. Furthermore, in practice, the pulse width t_p will be elongated by the laser beam size at the receiver.

 

In conclusions, the following results were obtained.

 

(1) The system is highly accurate, i.e., exceeds 95% accuracy.

(2) The system shows very high resolution for the torsion angle, that is, the smallest  measurable torsion angle is 1.210^-4 rad for a rotational frequency of 260 and an oscillator frequency of 1 MHz, which is more than sufficient for practical use.

(3) The system is relatively simple.

(4) The system can effectively be used for monitoring small changes in torsion in realtime.

 

 

References

 

1)  M. Ueda, S. Mizuno, & A. Matsumura: Realtime optical sensor for dye color and concentration detection. Rev. Laser Eng., 22-10(1994) p. 828. Ref. No. 7) in Chap. 4

 

2)  M. Ueda, S. Mizuno, A. Matsumura, & F. Sakan: Real-Time Optical Monitoring System for Dye Colour and Concentration. Opt. Lasers Eng, 25(1996) p. 13.

 

3)  M. R. Osborne, Nonlinear least squares-The Levenberg algorithm revisited. J. Australian Mathematical Society., 19 (1976) p. 343.

 

4)  M.Ueda, M.Kawazu and H.Suga: A laser system for cloth filaments, Opt. Laser Eng. 28(1997) p.71.

 

5)  M.Kawazu, M.Ueda and H.Suga: A practical system for counting cloth filaments by sheet like laser beam, Rep. Top. Meet. Laser Soc. No. RTM-97-3 (1997) p. 13.

 

6)  J. P. Den Hartog, Mechanical Vibrations, 4th Eds., McGraw Hill (1956).; O. Taniguchi & S. Fujii, Trans. (1998), Corona, p. 63.

 

7)  R. J. Collier, C. B. Burckhardt, & H. L. Lawrence : Optical holography, Academic Press (1971) p. 438.

 

8)       Eds. K. Takahashi, etc., Handbook for the Sensors, Asakura (1991) p. 324.

 

9)  JSME ed.: Mechanical Engineers' Handbook, Jpn. Soc. Mech. Engrs. (1987) A4-43.

 

10)  M. Ueda, T. Yamaguchi, J. Chen, K. Asada, K. Taniguchi, and H. Suga, "An optical method for detecting torsion in a power transmission shaft in realtime", Rev. Laser Engr., 26-11(1998) p. 821.

 

11)  M. Ueda, T. Yamaguchi, J. Chen, K. Asada, K. Taniguchi, and H. Suga, "An optical system for monitoring torsion in a power transmission shaft in realtime", Opt. Laser Engr., 31-3(1999) p. 199.

 

[Chapter 5 Part II will be presented in the upcoming September-October 2010 issue of this Journal.]