Fundamentals and Practices of Sensing Technologies
by Dr. Keiji Taniguchi, Hon. Professor of Engineering
University of Fukui, Fukui, Japan
Xi’ an University of Technology, Xi’ an, China
Dr. Masahiro Ueda, Honorary Professor, Faculty of Education and Regional Studies
University of Fukui, Fukui, Japan
Dr. Ningfeng Zeng, an Engineer of Sysmex Corporation
(A Global Medical Instrument Corporation), Kobe, Japan
Dr. Kazuhiko Ishikawa, Assistant Professor
Faculty of Education and Regional Studies, University of Fukui, Fukui, Japan
[Editor’s Note: This paper is presented as Part VII of a series from the new book “Fundamentals and Practices of Sensing Technologies”; subsequent chapters will be featured in upcoming issues of this Journal.]
Chapter 3 (Section II):
Some Practical Examples of Recent Ceramic Sensors
3.5 Acoustic Transducers
3.5.1 Structure of Acoustic Transducer (1)-(4)
Fig. 3.16 shows the structure of an acoustic transducer using piezoelectric ceramic element. This transducer can radiate acoustic wave in a medium of space by means of the electrical signal. Therefore, the piezoelectric ceramic transducer is used as a radiator of the acoustic wave. This transducer can, also convert some of acoustic wave propagated in a medium of space into the electrical signal. Therefore, the piezoelectric ceramic transducer is used as the acoustic sensor.
The backside of this element is filled with an acoustic absorbing material to absorb acoustic energy propagated to the backside.
 |
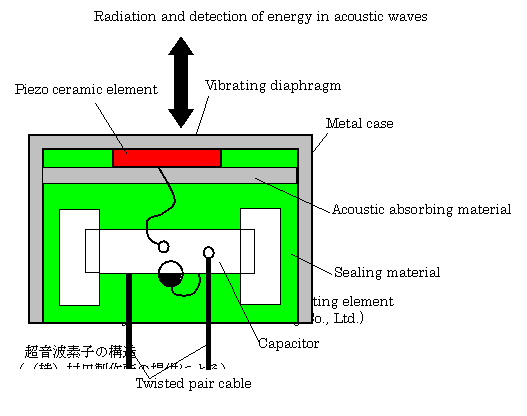A capacitive deviation of the piezoelectric ceramic element due to temperature changes can be compensated by means of the capacitor implemented in a metal case shown in this figure.
3.5.2 Equivalent Circuit for Acoustic Transducer (5)
Figure 3.17 shows the equivalent circuits for the piezoelectric ceramic element and a parallel resonant circuit for a receiver using this transducer.
 |
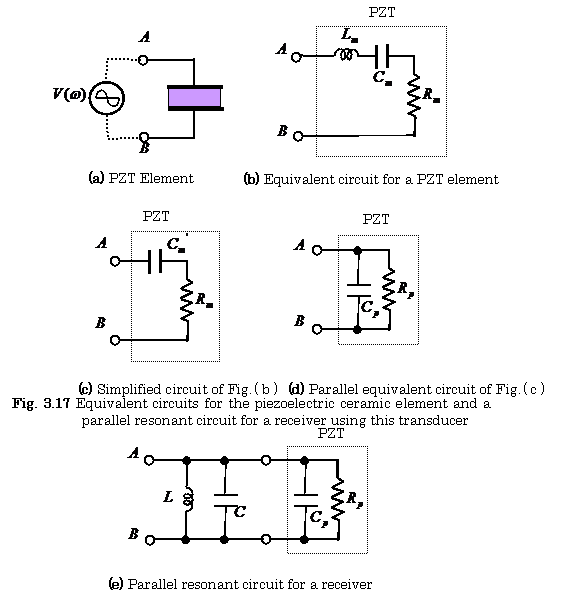Figures 3.17 (a) and (b) are the piezoelectric ceramic element and its equivalent circuit, respectively.
Figure 3.17 (c) is a simplified equivalent
circuit in the frequency range of 
for the circuit shown in Fig. (b), where 
.
Figure 3.17 (d) is a parallel equivalent circuit of Fig. (c),
where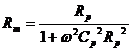 
, 
.
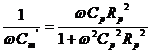Figure 3.17 (e) is a parallel resonant circuit of a receiver used for suppressing reverberations.
The resonance angular frequency 
of
the parallel resonant circuit is, then expressed
as follows:
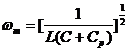
where 
is an inductance of the
receiving circuit.
The overall characteristic
for two parallel capacitors
,
(
: Temperature) in the
parallel
resonant circuit is almost independent for the change of
temperature.
3.5.3. Principle of Distance Measurement (1)-(4)
Figure 3.18 shows a block diagram for transmitting and receiving circuits using the transducer. This system consists of two sets of these circuits.
Firstly a timing generator is triggered by a start signal from the CPU, and
a rectangular pulse is generated. This pulse is amplified by a transmitting signal amplifier and is then sent to an acoustic transducer which transforms from the electric power to the acoustic power.
Secondary, this acoustic signal is radiated into a medium of space, and reflected and scattered waves from the medium are propagated toward the transducer of the original position as echo signals.
Finally, the received signal on the transducer is amplified and reformed into the pulse waveform.
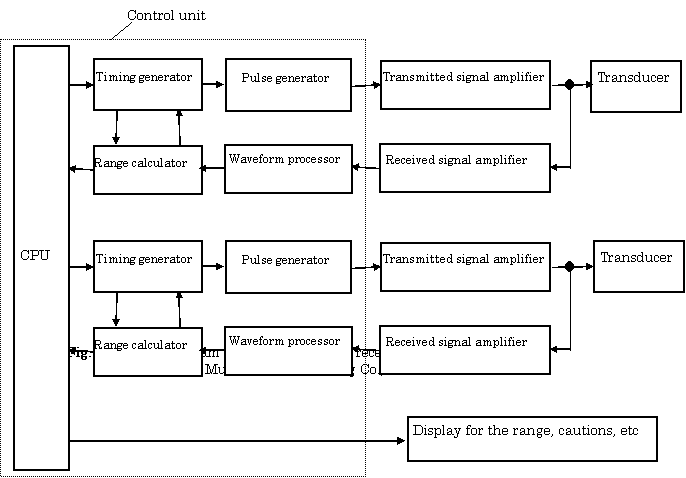
Figure 3.19 shows a transmitted signal and a
received (echo) signal. The round-trip time of
the transmitting signal
is measured as a number
of clock pulses, and the distance 
between an object and
the transducer, is calculated by the following formula:
（３．1）
where 
is the
propagation velocity of the transmitted signal, 
is the clock pulse
repetition period, 
is a number of clock
pulses included in .
These details are described in section1.3 in chapter 1.
 |
3.5.4 Important Characteristics for Automobile Sensing Systems (1)-(4)
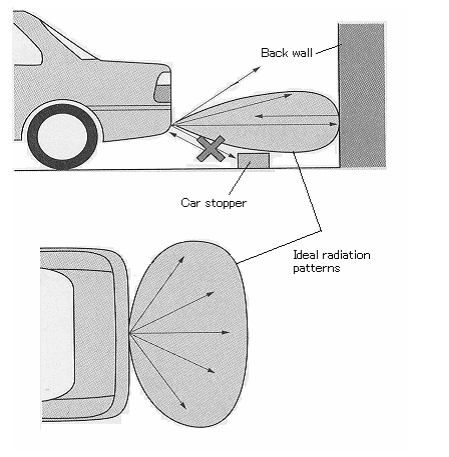
Important characteristics as a back acoustic sensor used for automobile sensing systems are as follows:
(1) The acoustic signal from the back wall must be detected, and that from the stopper must not detected as shown in Fig. 3.20(a).
(2) The horizontal directivity must have a wide radiation pattern, and the vertical directivity must have a sharp radiation pattern
as shown in Figs.3.20 (a) and (b).
|
3.5.5 Application Examples of Transducers (1)-(4)
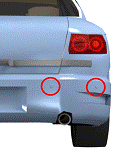
Figure3.21 shows an example of four back acoustic sensors used for an automobile.
A large number of sensing systems can precisely measure the position of objects.
|
||||
|
||||
3.6 Piezoelectric Vibrating Gyro Sensor(1)-(4)
3.6.1 Outlines of Sensor
A gyro sensor is used for measuring an angular velocity of an object. This sensor converts the angular velocity into an electrical signal.
3.6.2 Vibrating Gyro Sensor Elements
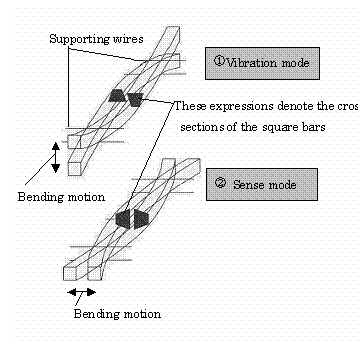
As shown in Fig. 3.21(a), a square
bar vibrates caused by a vibrating PZT along the direction of 
axis,
and its vibrating pattern, i.e., vibration mode, is shown in Fig. 3.21(b)-①. In a sense
mode shown in Fig.3.21(b)-②, when the vibrating gyro sensor rotates to the clockwise
direction as shown in Fig.321(c), a sensing PZT fixed to perpendicular for 
axis
of the square bar shown in Fig. 3.21(a) has an output voltage
.
The voltage which is
caused by the Corioli’s force
, is proportional to the
angular velocity 
. The force acts
on the cross section of the square bars as illustrated in Fig.3.21 ( c ) . The
gyro sensor converts the angular velocity into the output voltage.
Wires for supporting square bar are
positioned to the nodes of vibration of square bars as shown in
Fig. 3.21 (b). The relationships among the angular velocity , the
vibrating velocity 
, and the Corioli’s
forceis expressed as follows:
（３．２）
where 
is the mass of the
square bar.
 |
 |
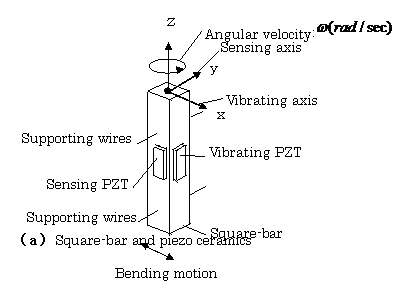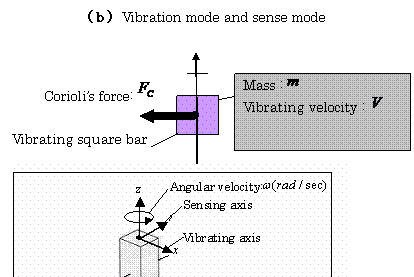（ｃ）Relationships among vibration, rotation, and Corioli’s force
|
3.6.3 Relationships between Input and Output Characteristics of Sensor
The
output of PZT is linearly
proportional to Corioli’s force, and is then
given by the following equation from equation (3.2),
.
(3.3)
where 
is
the proportional constant, and 
.
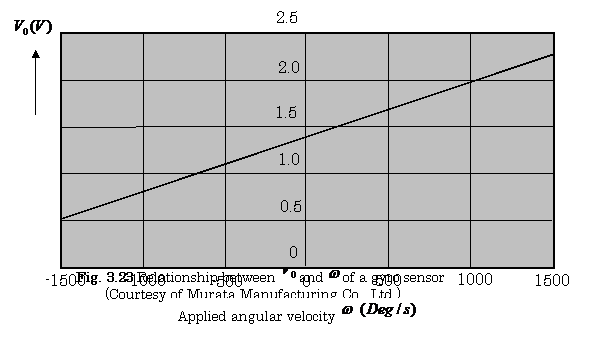
Figure
3.23 shows an experimental result between the angular velocity applied,
and the output voltage of the gyro-sensor. As
shown in this figure, there is the offset voltage
, and then the
relationship between and is
expressed
as follows:
(3.4)
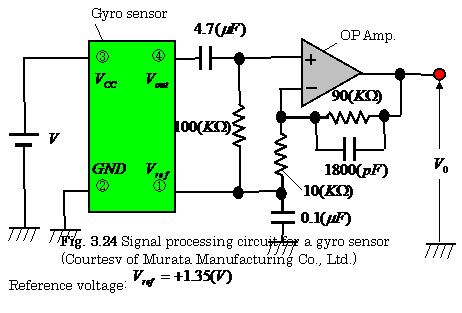
3.6.4 Signal Processing Circuit for Sensor
Figure 3.24
shows a signal processing circuit for the gyro sensor. The output
voltage
from
the gyro sensor is amplified to AVout by means of an AC- coupled
operational amplifier with the amplification factor A (In this case A=10) which
gives the final output = AVout, as
shown in this figure.
 |
3.6.5 Application Examples of Gyro Sensor
We show here two application examples of the gyro sensor.
(1) Figure 3.25(a) shows the gyro sensor used for a correction of azimuth in a global positioning system (GPS) implemented for the automobile navigation.
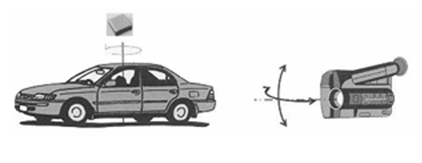
(2) Figure 3.25(b) shows the two gyro sensors used for two- dimensional corrections of the center of an image obtained from a video camera supported by unstable human hands.
|
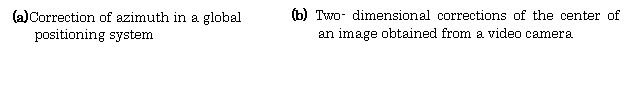
【References】
(1)Akira Murata : Wonderful stones, Nikkei Inc. (1994)
(2) Wonderful Ceramics (New materials and new technologies in 20th Century),
Supervised by Yutaka Takagi, Teturo Tanaka, Edited by Murata Manufacturing Co. Ltd, MARUZEN Co. Ltd(1990)
(3) Satoru Fujishima: Piezo-ceramics, Shokabo Publishing Co. Ltd (1993)
(4) Technical data for sensing devices (2007), Presented by Murata Manufacturing Co. Ltd.
(5) Metamorphosis,pp.8-9,No11（2005.12）, Edited by Murata Manufacturing
Co. Ltd.
【Problems and solutions】
3.1 Find the
output voltage in the circuit shown in
Fig.3.17.
【Solution】Let’s show again the circuit in Fig. 3.17.
 |
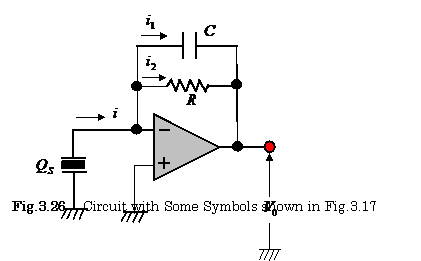In
Fig.3.26, 
, 
, 
, 
, 
.
>From these equations, we obtain the following
result:
.
In this equation,
(1) If 
,
then 
.
(2) The
frequency satisfying a condition of 
is 
, and then the
output voltage is 
.
3.2 Find the
output voltage , and a cut off
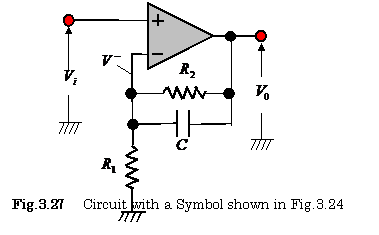
frequency in low frequency ranges in the circuit shown in Fig.3.27.
 |
【Solution】
The following equations can be obtained in the circuit shown in Fig.3.27.
, 
,
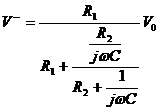(1) An output voltage is then expressed as: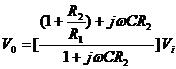 
.
(2) The
frequency satisfying a condition of 
is as follows:
3.3 Show a circuit diagram for measuring ranges (round- trip times).
【Solution】
We show a circuit configuration and a truth table of a R-S flip flop used in the circuit in Figs. 3.28 (a) and (b). We also show the operating waveforms of the R-S flip flop, an and- circuit, and a clock pulse generator in Fig.3.28(c).
 |
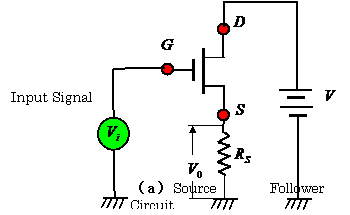
3.4 Find the
output
voltage in the circuit with a
FET shown in Fig.3.20.
【Solution】
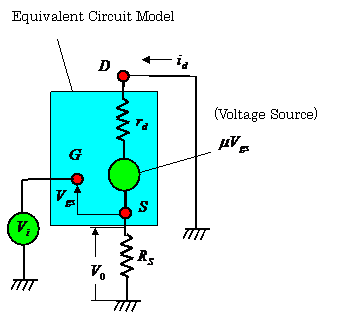
This circuit is well known as a source follower or a common drain circuit.
 |
The following equations are obtained from the equivalent circuit in figure 3.20 (b).
,
, 
The output voltage is
approximated as follows from these equations:
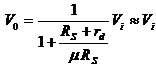
where 
expresses an
amplification factor, 
a drain resistance, 
a
drain current, 
a voltage between the
gate and the source, and 
a load resistance.
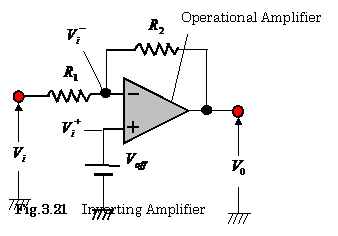
3.5 In the circuit shown in Fig.3.21,
(1)
Find an output voltage , when 
is
given as an input voltage. Where 
is an off set voltage.
(2) Find 
when the
output voltage is offset
free.
 |
【Solution】
(1) We obtain the following equations using Fig.3.21.
, 
, 
The output voltage is,
then, obtained as follows:
(1)
(2) Inserting into Eq. (1),
the output voltage is expressed
as follows:
(2)
The required condition is as
follows, for which the output voltage is offset free:
受信パルス
,
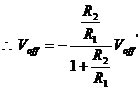(3)
[Chapter 4 will be presented in the upcoming May-June 2010 issue of this Journal.]
[ BWW Society Home Page ]
© 2009-2010 The Bibliotheque: World Wide Society