Fundamentals and Practices of Sensing Technologies

by Dr. Keiji Taniguchi, Hon. Professor of Engineering

University of Fukui, Fukui, Japan

Xi’ an University of Technology, Xi’ an, China

Dr. Masahiro Ueda, Honorary Professor, Faculty of Education and Regional Studies

 University of Fukui, Fukui, Japan

Dr. Ningfeng Zeng, an Engineer of Sysmex Corporation

(A Global Medical Instrument Corporation), Kobe, Japan

Dr. Kazuhiko Ishikawa, Assistant Professor

Faculty of Education and Regional Studies, University of Fukui, Fukui, Japan

 

[Editor’s Note: This paper is presented as Part XIII of a series from the new book “Fundamentals and Practices of Sensing Technologies”; subsequent sections will be featured in upcoming issues of this Journal.]

 

 

Chapter Six – Part I

 

Abstract for Chapter 6:

 

Many high technologies using opto-electronics have, recently, been developed, realized and used in the practical plants to manufacture a high quality product.

On the other hand, technologies using a simple physical principle, we call this "low technology", have, also, been used successfully. The representative examples using high technologies are the remote sensing technology and control technology in an atomic power plant and robot controlled machine in a semi-conductor industry. Some technologies described in Chaps. 4 and 5 and in this chapter are almost the examples using low technologies. These low technologies have the following merits.

(1) Almost all the measuring apparatuses are simple and economical.

(2) The apparatuses have, generally, a high durability and a high substantiality.

(3) The apparatuses can, easily, be used to many applications.

(4) The operation for the apparatus can, previously, be prepared.

In this chapter, the principles and features of some technologies using electro-magnetic fields are described. That is, a vacuum leakage sensor for pressure sensor in 6.1, a water amount sensor in glass fibers in 6.2, a pinhole sensor for glass wool paper in 6.3, a charge -to-mass ratio sensor for toner particles in 6.4, and an active sensor for bearing wear in 6.5.

 

6.1 Vacuum Leakage Sensor for Pressure Sensor

 

6.1.1 Introduction

 

Vacuum leakage of a pressure sensor used in the car often yields a serious problem even if the leakage is very small. The most sensitive and precise method now in practical use is a radio-isotope method. The method has, however, such problems as high cost and, in particular, environmental pollution. A new technique is then necessary to alleviate these problems.

In a previous paper¹⁾, we proposed a new method for detecting vacuum leakage using a pulse discharge technique. The principle is based on the discharge characteristics called Paschen's law²⁾, whereby the breakdown voltage of the discharge depends on the pressure. The results suggested that the method can be used in industry. It poses, however, some problems for practical use. Two of the serious problems are the lack of sensitivity and restriction to an applicable range of pressure of the sensor. These make the method difficult to use practically in industry. 

In this section, we report a new technique to solve these two main problems in order to make the method applicable in the industrial field.

 

6.1.2 Improvement on the Previous Method

 

A. Previous Method

 

The principle and the experimental method are basically same as that reported in the previous paper¹⁾. Figure 6.1(a) shows the experimental set-up used in the pressure-controlled simulation experiment and figure 6.1(b) shows the electrical circuit used to obtain the discharge characteristics of a single-shot discharge. The eight electrode pins embedded in the pressure sensor were used as an anode. They were connected to each other in order to maintain the same electrical potential. The shielding body case was used as a cathode. A high resistance (a few tens of mega-ohms) was used to restrict the discharge current and to avoid damaging the IC circuit in the sensor due to a high-voltage discharge and an electromagnetic relay, EMR, was used to obtain an one-shot discharge with a duration of about a few microseconds ( see Fig. 6.1(b)).

A simulation experiment was performed in order to obtain the discharge characteristics, that is, a relation between the discharge potential and the pressure, just like in the previous paper¹⁾. The experiment was performed using a pseudo-sensor, in which the shielding cap of the sensor can be removed. The removed cap re-connected to the base of sensor's body so that the electric field is the same as that of the practical sensor but the pressure in the pseudo-sensor can be easily controlled.

 

 

  

 

 

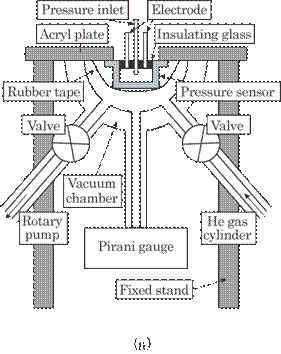
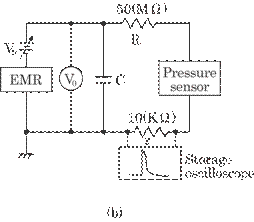
Fig. 6.1 The experimental arrangement. (a) The experimental set-up used to obtain the　

　　　　pressure-controlled simulation experiment and (b) electrical circuit for the　

single-shot discharge.

 

 

The discharge characteristics can be used for the estimation of pressure in the sensor, that is, to provide a measurement standard of the inner pressure. The method, therefore, requires two measurements after a proper time interval T in order to obtain the vacuum leakage rate.

 

B. Improvement

 

The accuracy of the estimation of pressure depends on the reproducibility of the discharge. The potential difference differs by about a few tens of volts around a mean value in each measurement even if the pressure could be maintained constant¹⁾. The difference, namely, fluctuation, of the discharge potential means that one requires a long time interval T, for example a week, in order to detect a maximum allowable vacuum leakage rate, in this case 110^-5 Pa・cm³s^-1. This was the main disadvantage and prevented the method from being practically used in the car industry.

In this study, we have made three improvements to reduce the fluctuation of the discharge potential. Firstly, electric conductive paste was used to keep a good electric connection between the eight electrical pins leading out and the high-voltage power line. Secondly, prior to an inspection discharge, a pre-discharge was carried out to flush the surface of the pressure sensor. Thirdly, the optimum speed of raising the potential from zero to the discharge potential was sought and found to be 30 Vs-1.

Another main disadvantage of the previous method was that the method can only be applied effectively within a narrow range of inner pressure, 70-150 Pa. This also restricts the method for applications in the industrial field because the usual inner pressure range is 70-300 Pa due to many factors involved in making the practical sensor. That is, our method is quite useless above 150 Pa, where it has little sensitivity, as is discussed in the next section. We have, however, found a new techniques using He gas to solve this problem. Addition of a small amount of He gas has a large effect on the discharge. It makes the method useful in the pressure range above 150 Pa.

 

6.1.3 Results and Discussions

 

A simulation experiment was performed to obtain discharge characteristics using three pseudo-sensors, A, B and C. Figure 6.2 shows an example of the discharge characteristics for sample A in the pressure range 70-150 Pa. This is the well-known Paschen law²⁾, which has been obtained by using an ordinary discharge. The fluctuation of the discharge potential, namely the differences between maximum and minimum values, in ten measurements were all below 70 V at any given pressure. The other two samples, B and C, have also almost the same fluctuation as that of sample A in the pressure range 70-150 Pa. These fluctuation are considerably reduced to about a half the original value of the previous one without the improvement.

It is generally believed that the discharge potential fluctuates greatly and it is essentially difficult to use this method for estimation of pressure within high precision. It is, however, supposed that, under limited conditions, the fluctuation of the discharge potential can be decreased to a considerable extent. In this experimental case, the discharge is supposed to occur on the surface of glass which is used as an insulator between the electrode pins and the base metal of the pressure sensor. This was proved by the fact that the discharge potential is almost the same even when the shielding cap was removed in the simulation experiment. The method has thus been proved to be suitable for use in industry.

 

 

 

 

 

 

 

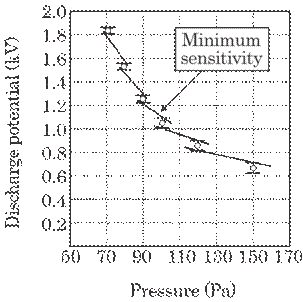
Fig. 6.2 Discharge characteristics for a pseudo-sensor sample. Ten measurements were performed for each pressure.

 

 

Figure 6.3 shows the discharge characteristics for three pseudo-sensor samples in the pressure range 70-500 Pa. The discharge potential is a mean value. These characteristics almost coincide with each other. There is, however, a little difference for each sample. This causes a problem regarding which characteristic curve is used when the pressure of practical sensor is estimated from the measured discharge potential.

It is useful to define a sensitivity S as follows for evaluation of the method in practical use.

 

(6.1)

 

Where V is a small change of discharge potential due to a small change in pressure, p. The sensitivity depends strongly on the pressure, as can be seen in Figs. 6.2 and 6.3. A large S means a high sensitivity in estimating the pressure from the discharge potential. It is natural to use a mean sensitivity, mean S, which is obtained from the averaged discharge potential at each pressure. In the previous paper, we used the mean sensitivity. It may, however, be more useful to use the minimum sensitivity to find out for certain the maximum allowable leakage rate of the sensor, R_m. That is, this never misses leakage rates lager than R_m and is essential for industrial use from the viewpoint of safety planning. The minimum sensitivity, S_min, can be obtained from the straight line shown in Fig. 6.2. The standard R_m now used in the car industry is 110^-5 Pacm³s^-1, which is obtained from consideration of a car life time of about 15 years.

 

 

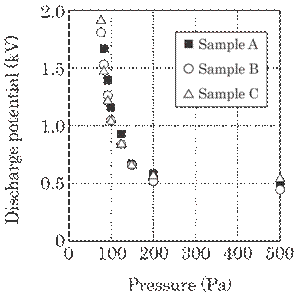
Fig. 6.3 Discharge characteristics for three typical sensor samples. The value at each pressure is the mean values of ten measurements.

 

 

Table 6.1 shows the minimum sensitivity for three pseudo-sensor samples, A, B and C, one of which is obtained from Fig. 6.2. The blank column for sample A means that the discharge did not take place even at 2000 V, which is the maximum supply voltage in this experiment. The error in pressure due to the fluctuation of the discharge potential can be determined by the values in table 6.1.

 

 

Table 6.1 Minimum sensitivities S defined by S_min=|V_min/P|, where V_min is the minimum difference between the discharge potentials in each pressure range and P is the difference in pressure.

 

 

 

Table 6.2 shows the discharge potential of the practical pressure sensors. Two kinds of sensor were used: one has high discharge potential, 1100-1500 V, which means that the inner pressure of the sample is estimated to be relatively low, 80-100 Torr, as can be seen in Fig. 6.3, whereas the other has a low potential, 500-600 V, namely a high inner pressure of around 150-200 Torr.

 

Table 6.2  Some examples of discharge potentials observed in 16 practical sensors. The fluctuation of the discharge potential is shown as the peak-peak (P-P) value. Two kinds of sensors were used; one has a high discharge potential and the other has a low discharge potential.

 

 

 

Ten measurements were performed for each sensor. The maximum fluctuations of the discharge potential, V_p-p, were all smaller than 25 V for this kind of low-pressure type. The fluctuation was, however, about 40 V for the high-pressure type. A rather small fluctuation can thus be obtained by implementing the improvements mentioned in 6.1.2.B. The fluctuation causes a presumed error in pressure. The reduction of this fluctuation is one of the most important factors for this method to be effectively used in the industrial field. That is, the error can be used as a standard for a clear distinction of vacuum leakage from error in pressure. The presumed error in pressure depends also on the sensitivity mentioned above. For an example, the error in pressure can be calculated to be 2.4 Pa(=25/10.4) for the

fluctuation potential of 25 V and the minimum sensitivity of 10.4 VPa^-1. The presumed error in pressure, finally, determines the accuracy of this method, in other words, determines the shortest time required in order to detect the allowable maximum leakage rate. The required time can, thus, be determined from the presumed error in pressure due to the potential fluctuation, the minimum sensitivity, the allowable maximum leakage rate and the sensor's volume.

The increase in pressure can be calculated to be 1.7 Pa per day if the sensor leaks with the maximum leakage rate of R_m = 110^-5 Pacm³s^-1 and the sensor's volume is 0.5 cm³. For example, the time required can, then, be calculated to be 1.39(=2.4/1.7) days for the presumed error in pressure of 2.4 Pa.

Table 6.3 shows the presumed error in pressure and table 6.4 shows the required time in days for these samples, A, B and C, and various pressure ranges. These are used for the measurement standard of this method.

The values, however, differ slightly from each other. We, may, therefore, use a smaller sensitivity and then a longer detecting time in order to take a safe measurement. From the practical point of view, the time interval T between the two measurements to obtain the vacuum leakage rate should be less 3 days. Therefore, it is concluded from tables 6.3 and 6.4 that the method can only be useful for the pressure range 70-150 Pa; an example of this is sensors 1-8 in table 6.2.

 

 

Table 6.3  The sensitivity of this method in terms of the estimated maximum error in pressure caused by a fluctuation in potential of 25 V.

 

 

 

Table 6.4  The sensitivity of this method in terms of the minimum number of days required in order to detect the maximum allowable leakage rate of 110^-5 Pacm³s^-1 for a practical sensor.

 

 

 

The sensitivity decreases abruptly when the inner pressure is over 150 Pa.  That is, the method cannot be applied to a sensor with an inner pressure above 150 Pa; an example of this pressure range is sensors 9~16 in table 6.2. The lack of sensitivity is an unavoidable disadvantage of this method. We have, however, found a new phenomenon allowing us to solve this problem. Namely, the sensitivity can be increased by employing He gas, instead of air, as the surrounding gas of the sensor.

Table 6.5 shows the relation between the discharge potential and the total inner pressure for a sensor filled with air and He gas. As shown in Fig. 6.3, the discharge potential surely decreases as the inner pressure increases in the pressure range 70-500 Pa. It was, however, found that addition of He gas increases the discharge potential and the amount of the gas determines the increase in potential. We can then devise a sensor with a pinhole for gas flow.

 

 

Table 6.5 The effect of He gas on the discharge characteristics.

 

 

 

For this purpose, sensors with a high pressure, above 150 Pa, namely a low discharge potential must be set in a chamber filled with only He gas for a few days. A detailed experiment and a theoretical analysis will be required for the determination of the leakage rate.

Only a theoretical analysis for the leakage rate of each gas was performed for the estimation of the amount of each gas that leaked into the sensor. Figure 6.4 (a) shows a conceptual expression for the pinhole and Fig. 6.4(b) is for gas leakage. Two chambers are isolated by a wall with a small pinhole; one is maintained at vacuum and the other at atmospheric pressure.

The basis of the theory is to calculate the dimension of the pinhole for a given leakage rate and the amount of gas being leaked through the pinhole. The amount of gas leaked, N, can be expressed, from a consideration of thermo-statistical mechanics³⁾, as

 

(6.2)

 

where n is the number density of gas molecules, S is the cross-sectional area of the pinhole and V is the thermal velocity.

 

 

 

Fig. 6.4 A schematic diagram of the gas leak. (a) a model of the pinhole and (b) the concept of gas leakage.

 

 

S can be calculated to be

 

(6.3)

 

assuming a maximum allowable leakage rate of R_m = 110^-5 Pacm³s^-1. If the area is assumed to be a disc, the diameter D can be calculated to be

 

(6.3)'

 

Molecular diameters d of He, N₂ and Kr are given as follows⁴⁾,

 

(6.4)

 

N₂ gas is considered as air in this case. The effective cross sectional area C by which each molecule goes past the pinhole without colliding with a wall, therefore, can be obtained as,

 

	(6.5)

 

The leakage rate R is directly proportional to this effective cross sectional area and the mean thermal velocity V which can be calculated to be V_He = 1.367 kms^-1, V_N2 = 0.516 kms^-1, V_Kr = 0.299 kms^-1 assuming a room temperature T = 300 K. We can, then, obtain the relation of the leakage rates of each gas, as follows:

 

(6.6)

 

The result shown above was obtained by assuming that the pinhole is just a disc in shape. The actual shape of the pinhole may be an ellipse and the ratio may become larger than that of Eq. (6.6). Therefore, it is assumed that the inner pressure due to leakage of gas into the sensor increases faster for He than it does for air by a factor of about a few tens. As a result, the increase in pressure during a day is expected to be about 30-50 Pa(=1.71R_He/R_N2) for the maximum allowable leakage rate of R_m = 110^-5 Pacm³s^-1. This amount of gas pressure increment would sufficiently increase the discharge potential, as can be seen from table 6.5. This makes the method effective even in the pressure range above 150 Pa. The reason why the addition of He increases the discharge potential remarkably compared with the case for air may be due to the fact that the ionic potential of He (24.58 eV) is far higher than that of N₂ (15.58 eV).

The most sensitive method now used for the detection of air leakage is a radio-isotope method. It requires about 2 days to detect the maximum allowable leakage rate of R_m = 110^-5 Pacm³s^-1 clearly. The method may, however, have a problem from the consideration mentioned above, namely that air leaks although Kr does not leak when the cross section of the pinhole is not a disk but rather a hole with the shape of a long and narrow ellipse.

 

In conclusions, the following results were obtained.

 

(1) The new method using the discharge technique has been developed to detect the vacuum leakage of the pressure sensor.

(2) The applicable pressure range is extended from 70-150 Pa to a few hundred Pa by employing He gas as the surrounding gas to detect the leakage.

(3) The efficiency of this method is equal to or higher than the radio-isotope method now in practical use.

 

 

 

 

 

6.2 Water Amount Sensor in Glass Fibers

 

6.2.1 Introduction

 

Recently, various techniques based on opto-electronic engineering have been developed and applied to many production processes in factories for checking the product quality. However, an idea based on a simple and classical physical principle is sometimes still very useful even under conditions where modern techniques are not so effective or are quite powerless. Also, another advantage of a simple and classical method is its low cost. In a previous study⁵⁾, we proved that a pulse discharge technique, though it is a very old technique in science, is very useful to detect the leakage of pressure sensors.

In this study, the property of static electricity was shown to be successfully applied to detecting the water amount on the surface of glass fibers. Recently there have been many demands for glass fibers in industrial fields not only for use in optical fibers but also for materials with various functions. One of them is the application to a separator for a lead-sulfuric-acid battery. This kind of fiber has a homogeneous structure. The glass fiber was produced from melted glass by being pushed out of a nozzle. The molten glass was immediately cooled by exposure to a shower of cold water to form a thin fiber (20 m in diameter), and it was rolled on a spindle. The fiber was cut to about 3 m in length and formed into a bundle. The bundle of glass fibers was then dried to reduce the water on the surface to a suitable level. The presence of adequate water on the surface of the glass fiber is very important when fabrication of the separator is done. The best condition for the water content is known to be in the range between 0.1 and 0.3 weight percent. The weight of water attached on the surface of the glass fiber can be calculated by subtracting the net weight of the glass fiber which is obtained after being completely dried. However, the method takes time, thus it was not often used on a practical basis. Usually in the production stage in factories, skilled persons check the water amount based on their intuition when they touch the fibers with their fingers. Therefore, development of a new method for detecting the water on the surface of glass fibers has been required in the industrial field. In the case of water in the atmosphere, we can employ an infrared absorption method. However, this method cannot be applied in this case because the glass itself has a high absorbance in the infrared spectral region. Also, the Raman spectroscopic technique is impractical in factories because of its high cost.

   In this section, we propose a very simple and practical method for measuring a water amount in the glass fibers by means of a static leakage current.

 

6.2.2 Principle and Method

 

In a preliminary experiment, a leaf-electrometer was used to examine how the water on the surface of the fibers influenced the leakage of static electricity stored in the leaf-electrometer. As a result, it was proved that, depending on the humidity in the room in which the fiber bundle was placed and also on the time it was left in the room, leakage current characteristics were quite different when the fiber bundle was touched by the electrode of the leaf-electrometer. Namely, when the humidity was high, the leaf of the leaf-electrometer soon closed. However, when the fibers were completely dried in a dry box, the leaf of the leaf-electrometer did not close, showing essentially no electrical conductivity. Such a phenomenon is essentially the same as that well known as the leakage of the static electricity. It is believed that ions such as Na⁺ are easily produced with the aid of water present on the surface of the materials and contribute to the electrical conduction⁶⁾. Prior to this experiment, we tried to use a conventional meg-ohm meter which is normally used to check for electrical insulation. However, the meter proved to be useless when the water amount on the glass fiber to be measured was lower than about 0.5%, showing infinite resistance.

In order to measure the transient leakage current, simple and compact equipment was designed and constructed. Figure 6.5 shows the schematic diagram of the equipment. The

 

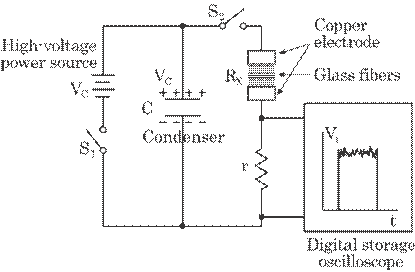
Fig. 6.5 Experimental setup used to measure the leakage current of static electricity flowing on the surface of glass fibers.

 

bundle of fibers was sandwiched between two electrodes. A high-voltage power source used for a flash lamp in a commercial disposable camera was used in this experiment. First, capacitor C (about 400 F) was charged up to around 400 V by the high-voltage power source. The charge of static electricity flows through the surface of the fiber when switch S₂ was turned on immediately after the switch S₁ was disconnected. The leakage current can be calculated by the pick-up voltage detected with the resistance r; the resistance value was changed in the range from several tens of k to several hundred k, depending on the water amount. The pick-up voltage was detected using a digital storage oscilloscope.

The current value varies with the thickness of the bundle of fibers and also with the pressure applied to the electrodes. The thickness of the bundle was kept constant at 10 mm in this experiment because this is the thickness during the production of the fibers. The illustration of the electrodes is shown in Fig. 6.6(a). Two copper-clad boards (size, 100150 mm) were used for the electrodes. Each of the electrodes was stacked on a plastic plate (10060010 mm). In order to supply almost constant pressure when the electrodes sandwiched the fiber bundle, a rubber band was used. Figure 6.6(b) shows an illustration of how the electrodes sandwich the fiber bundle during the measurement. The gap between the

 

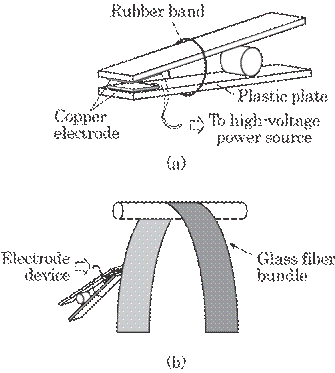
Fig. 6.6 (a) Illustration of the electrodes used for sandwiching the glass fibers and (b) illustration showing how the electrodes encompass the fiber bundle.

 

two electrodes was expanded once, and the fiber bundle was sandwiched while hanging during the drying process. Subsequent to sandwiching the glass fibers, the electrical current started to follow and immediately attained a maximum value within a few hundred milliseconds. Therefore, the measurement was finished within a short time of about 0.5 s.

In order to obtain an accurate measurement of the water attached on the surface of the fibers, the weight of the bundle of fibers was measured twice, namely once just after the leakage current measurement, and again after being completely dried for 30 min in a desiccator box. The water amount was calculated from the difference in weight.

 

6.2.3 Result and Discussions

 

Figure 6.7 shows a typical oscilloscope trace obtained from the experiment shown in Fig. 6.5. The trace shows almost no decay. This is because the charge stored in capacitor C is considerable, and the current flowing in the circuit is as low as A in magnitude.

 

 

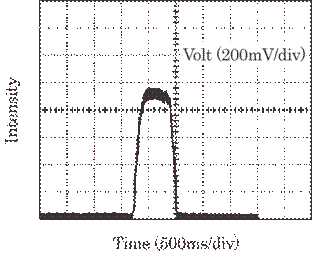
Fig. 6.7 Typical oscilloscope trace obtained from the experiment shown in Fig. 6.5.

 

Figure 6.8 shows the relationship between the water amount on the fiber surface and the

leakage current. Many samples containing various amounts of water from 0.08 to 1.2% were used in this experiment. A linear relationship was observed.

As described above, the best condition for the water amount on the surface of the fiber is in the range between 0.1 and 0.3 weight percent. Therefore, on the basis of the results shown in Fig. 6.8, we can say that this method can be practically applied to the measurement of water on the surface of the fibers.

It was also observed that when the pressure applied to the electrodes increases, the slope of the straight line in Fig. 6.8 increases. This is probably due to increased pressure causing better contact among the fibers and as a result, the actual path length of the fibers between electrodes became short.

In conclusions, the following results were obtained.

(1) The leakage current shows an almost linear relation to the water amount in the range between 0.08 and 1.2 weight percent.

(2) This method can be applied in factories as a highly sensitive, real-time method of determining a small amount of water attached on the fiber surface.

 

 

 

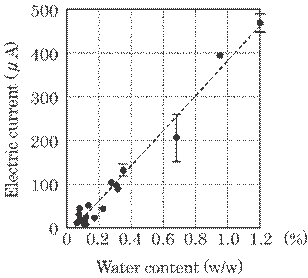
Fig. 6.8 Relationship between the water amount on the surface of glass fibers and the leakage current.

 

 

6.3 Pinhole Sensor for Glass Wool Paper

 

6.3.1 Introduction

 

Hitherto glass has generally been employed in the format windows, glass tubes and vessels. It has recently proved useful as an adiabatic mat, a soundproof mat, and a dustproof filter, all owing to the technical development of glass wool production. These mats have been used widely in cars and buildings, and the filter has been used in a semiconductor production factory. The functional efficiency of each product depends largely on the manufacturing process, i.e., the product is affected by factors of weight density, g/m², and the mean fiber diameter of the raw glass wool. We have developed a practical system for measuring the weight density in real time^7),8), and using an optical sensor to gauge the mean fiber diameter⁹⁾.

When the glass wool is to be used for a dustproof filter, in addition to these factors, the pinholes have to be detected and removed. Heretofore, CCD camera has been used for purposes of pinhole detection. This apparatus cannot, however, detect a pinhole of diameter smaller than approximately 0.5mm, and, further, is too costly for practical use.

We propose here a practical method for detecting a pinhole in real time. The principle of this method is based on the discharge phenomenon, whereby the breakdown voltage slightly decreases at a pinhole. This method of detection demonstrates high sensitivity, and the system is very simple and cheap enough for practical use.

 

6.3.2 Principle and Experimental Method

 

The breakdown voltage for pinhole detection depends on the permittivity of the material between the two electrodes. That is, the breakdown voltage changes when a glass wool paper were inserted between the two electrodes.

Figure 6.9 shows the electric circuit for the experiment. A negative high voltage was applied to the needle-shaped cathode. A metal roller was used as an anode which was connected to earth electrically from the practical point of view. A high resistance, R, was connected in series to the circuit to control the current; it does not affect the breakdown voltage, as discussed in section 6.3.4. In addition to this high resistance, two low resistances, r and r_s, were also connected in the circuit in series. Both the resistance r and r_s are used to detect electric discharge. The resistance r_s gives an alarm and r puts the discharge on record. The capacitor C is charged by the power supply. Once a discharge takes place between both electrodes, i.e., anode and cathode, a discharge current flows, and the voltage between these electrodes decreases in an instant, and finally the discharge stops. An electric power source, however, charges the capacitor within 0.3 ms.

 

 

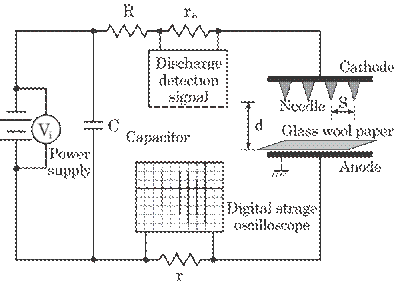
Fig. 6.9 Electric circuit for the discharge method.

 

Figure 6.10 shows the illustration of pinhole detection. Essentially, the practical advantage of this method is that the discharge voltage for air, V_D, is lower than that for the glass wool paper, V_P. The source voltage for pinhole detection, V_d, has, therefore, to be chosen between V_P and V_D. Thus the breakdown will take place only at the pinhole, which, in conclusion, suggests the existence of pinhole.

 

 

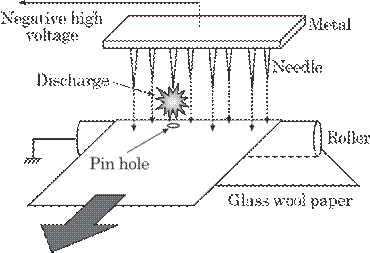
Fig. 6.10 Illustration of pinhole detection by means of electric discharge.

.

 

The breakdown voltage is determined by the strength of an electric field, which, in concrete terms, consists of the following: a permittivity between two electrodes; a distance between these electrodes, d; equidistant separation between needles constituting a cathode, s; a pinhole size to be detected, ; and a moving velocity of the glass wool paper, v. Another practical factor to be considered in industrial use is the deviation of the pinhole from a point just below the needle head, p, which may slightly increase the breakdown voltage. These will be discussed in sections 6.3.3 and 6.3.4.

 

6.3.3 Experimental Results

 

All the factors affecting the discharge voltage were examined in an effort to establish the acceptable conditions for practical application of this method.

First of all, we examined the effect of glass wool paper on the discharge voltage. Figure 6.11 shows the relation between discharge voltage, V_D, and the thickness of the paper, t. The distance between cathode and anode, was d=3 mm. The discharge voltage increases approximately linearly with the thickness of the glass wool paper. From the figure, the dielectric strength for air was found to be about 1.2 kV/mm (= 3.6/3), while that for the glass wool paper was about 2.5 kV/mm( = (9.2-5.2)/(2.4-0.8)). This enables us to use the method practically; i.e., the discharge will only take place at the pinhole under the condition of proper voltage.

 

 

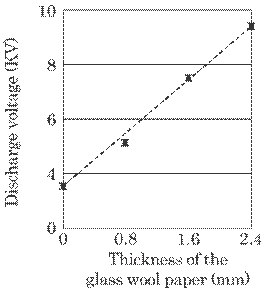
Fig. 6.11 Relation between the discharge voltage and the thickness of glass wool paper for s = 4mm, d = 3mm, and p = 0 mm.

 

 

Secondly, we examined the discharge characteristics by means of a digital oscilloscope. Figure 6.12 shows this example. The experimental conditions were d = 4 mm, s = 4 mm, V_D = 5.8 kV, R = 100 k, = 1.2 mm, t = 0.8 mm, p = 0 mm, and v = 50 mm/s. It was found that

 

 

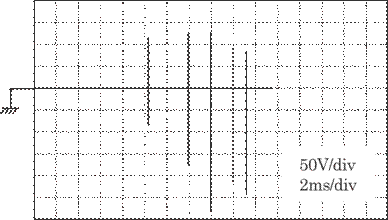
Fig. 6.12 Discharge characteristics. Discharge conditions: separation between needles is S=4mm; distance between anode and cathode is d=4mm; and discharge voltage is V_D=5.8 kV.

 

the discharge takes place intermittently at a period of about a few ms and the duration of the discharge was about 10 ms, and further the discharge voltage acquires negative as well as positive values, while one should expect either one or the other. This suggests that the rest of the system acts as a capacitance. The discharge voltage of 5.8 kV in Figure 6.11 is an estimate, calculated as follows: 2.50.8 + 1.23.2 = 5.84. Many similar experiments were carried out under various discharge conditions. The discharge characteristics were comparable under all experimental conditions. Acceptable conditions for a practical use of this pinhole detection method will be obtained from the results of these experiments.

Table 6.6 represents the discharge voltage when the pinhole was placed just below the needle cathode, and Table 6.7 the discharge voltage when the pinhole was shifted 1 mm for s = 2 mm, 2 mm for s = 4 mm, and 3 mm for s = 6 mm. That is, the pinhole was placed in the middle, between the needles. In this table, (a) shows the results obtained for R = 0, and (b) those for 100 k. As is well known, discharge is an uncertain phenomenon in the sense that it depends on such microscopic conditions as a surface condition and a surrounding condition as well as such the macroscopic conditions as a discharge voltage, a distance between electrodes and a resistance for the discharge. That is, each discharge occurs at slightly a different discharge voltage even though these macroscopic conditions are maintained. Thus each datum in these tables represents the mean value of ten measurements. The error of the

 

Table 6.6 Discharge voltage for various discharge conditions when the pinhole was just below the needle, each value is a mean value for ten measurements.

 

 

 

Table 6.7 Discharge voltage for various discharge conditions when the pinhole was

shifted from the needle, each value is a mean value for ten measurements.

 

 

 

discharge voltage was in each case within 200 V from the mean value. The blank column in

the tables indicates that discharge did not take place even at the relatively high voltage of 8 kV. A mark of  indicates that the discharge occurred somewhere other than at a pinhole.

Tables 6.6 and 6.7 shows the mean discharge voltage, where the rate of detection of the pinhole, in other words, the rate of an occurrence of the discharge, was about 70 % for ten measurements. On the whole, these tables suggest the following.

(1) The high resistance R hardly changes the discharge voltage; that is, it will only control the discharge current. The effect of R on the discharge current will be discussed in section 6.3.4.

(2) Both the separation, s, and the pinhole size, , in these ranges have little effect on the discharge voltage, excepting a clear effect of needle separation on excess discharge as denoted by  in Table 2.

(3) Finally the experiment was carried out to examine the effect of a velocity of glass wool paper on the discharge voltage. It was found that the increase in velocity from 0 to 3m/min only increased the mean discharge voltage by about 300 V.

 

6.3.4 Discussions

 

The detection rate will depend on many factors, such as the distance between electrodes, d; separation between the needles constituting a cathode, s; the size of the pinhole to be detected, ; and the moving velocity of the glass wool paper, v.

 

A. Factors Affecting the Detection Rate

 

Two factors are connected with the electrode, i.e., d and s, which may have a notable effect on the detection rate since it strongly affects the electric field. They are discussed in (a) and (b) in this section. The other two factors are connected with the practical conditions, i.e.,  and v, which are discussed in (c) and (d).

 

(a) Distance between electrode, d

From a practical point of view, a large distance, d, is desirable; otherwise, the needle cathode may come in contact with the glass wool paper when the paper moves through that region because the paper rises to the surface occasionally due to a local lack of tension. However, a large distance needs a rather high discharge voltage, above 10 kV. A point of compromise for the acceptable distance in practical use was found between 2 and 4 mm, based on our experiments. Considering the element of strength of the electric field, the separation between needles, s, were set at s = 2, 4, and 6 mm, the experiments were conducted for various combinations of d = 3 and 4 mm, and s = 2, 4, and 6 mm, to establish the acceptable conditions for the practical pinhole detection. Each experiment was carried out for ten measurements.

A clear difference due to a change of d was not found within the tested range. We then chose d = 3 mm as a practical distance, i.e., acceptable distance in practical use.

 

(b) Separation between needles, s

It was found from these experiments that the shift amount of the pinhole from the needle point, just on the glass wool paper, p, remarkably affects the detection rate. The detection rate was about 60 % for both electrode s = 2 or 4 mm, even when the shift amount was s/2, which corresponded to maximum shift amount. On the contrary, the detection rate with the electrode of s = 6 mm was about 100 % when the pinhole was just below the needle, i.e., p = 0 mm; it was about 75 % when p = 1 mm; and, finally, it was 10 % when p2 mm. This shows an important aspect of design of the electrodes. That is, one of the most reasonable electrode designs may be the one shown in Figure 6.13, which has three rows of electrodes, each of which consists of many needles with a separation of s = 6 mm and the lines shifted 2 mm from each other. With this design, the shift amount, p, can then be p1 mm and a detection rate above 70 % can be obtained.

 

 

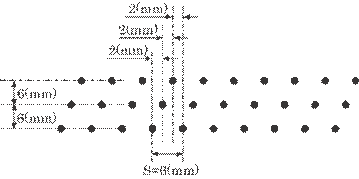
Fig. 6.13 Optimum arrangement of the needle electrode for practical use.

 

In this case, the roller diameter should be large enough compared to the spacing of the lines of needles. The practical roller diameter was about 300 mm, which was large enough for this purpose.

 

(c) Pinhole size,

The size of the pinhole to be detected was set between 0.1 and 0.5 mm.  Predominantly used sizes in these experiments were 0.1 and 0.3 mm. Sizes smaller than 0.1 mm, i.e., 0.05 mm, and larger than 0.3 mm, i.e., 1.0 mm were included to examine the effect of size on the detection rate. The detection rate for the size of 1.0 mm increased only about 10%. That is, pinhole size only slightly affects the detection rate.

 

(d)  Moving velocity of the glass wool paper, v

The increase in velocity increased the mean discharge voltage as shown in section 6.3.3, and then the moving velocity of the glass wool paper was fixed at v = 3 m/min, for experimental convenience. The practical velocity was, however, about 10 m/min. Preliminary experiments showed that the practical velocity of 10 m/min decreased the detection rate about 30 %. Thus the factor of velocity presents an identifiable problem for the practical application of this method in a manufacturing plant.

 

B. Effect of R on the Discharge Current and Voltage

 

Figure 6.14 shows an example of the discharge characteristics for R = 0, 1, 10, and 100 M. It is shown in this figure that changes in the high resistance R changes the discharge current. A continuous discharge has, albeit exceptionally, occurred even in the absence of a pinhole at about R = 10 M, and subsequently damaged the glass wool paper. A higher resistance than R = 100 M, such as 200 M, failed to cause a discharge. An optimum value of the resistance as expected from this experiment may be R = 100 M.

 

 

 

 

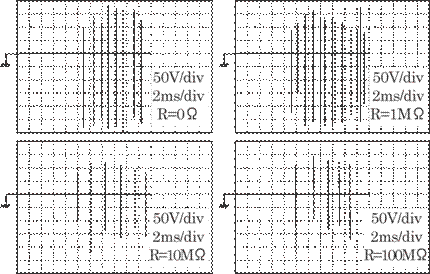
Fig. 6.14 Effect of high resistance on the discharge characteristics.

 

 

In conclusions, following results were obtained.

 

(1) Detectable pinhole size was between 0.1mm and 1.0 mm, and the detection rate was above 70% for the tested range of pinhole sizes.

(2) The production rate of inferior goods was reduced to approximately 33% by this method.

(3) These results were satisfactory for purposes of practical use, and the system has since been successfully implemented in a manufacturing plant.

 

 

References in Chap. 6 Part I:

 

1)  M. Ueda, K. Kagawa, Y. Sugino, K. Moriya, J. Chen, & T. Matsui: A new method for

detecting vacuum leakage of a pressure sensor using a pulse discharge technique, J. Phys. D: Appl. Phys. 30(1997), 703-707

 

2)  S. C. Brown: Introduction to Electrical Discharge in Gases (1996, New York: John Wiley and Sons) p. 3

 

3)  F. Reif: Fundamentals of Statistical and Theoretical Physics (1965, New York: McGraw-Hill) p. 269

 

4)  E. H. Kennard: Kinetic Theory of Gases (1938, New York: McGraw-Hill) p. 149.

 

5)  M. Ueda, K. Kagawa, Y. Sugino, K. Moriya, and T. Matsui, "A new method for detecting vacuum leakage of a pressure sensor using a pulse discharge technique", J. Phys. D: Appl. Phys., 30(1997) p. 703.

 

6)  W. R. Harper, Contact and Frictional Electrification, (1967) p. 76.

 

7)  J. Chen, M. Ueda, K. Asada, and K. Taniguchi, "Realtime Densitometer for Glass Wool Using Solar Cell," Opt. Laser Engr. 29(1998), p. 61.

 

8)  M. Ueda, J. Chen, K. Taniguchi, and K. Asada, "Realtime Densitometer for Glass Wool Using Solar Cell - for Industrial Use," Rev. Laser Engr. 26(1998), p. 328.

 

9)      J. Chen, Y.U. Lee, M. Ueda, K. Taniguchi, and K. Asada, "A Simple Optical Method for the Measurement of Glass Wool Fiber Diameter," Opt. Laser Engr. 29(1998), p. 67.

 

[Editor’s Note: This concludes Part I of Chapter 6; the final installent of this book, Chapter 6 Part II, will appear in the upcoming May-June issue of this Journal.]