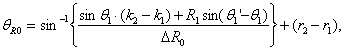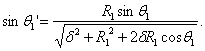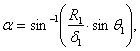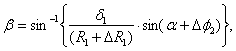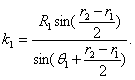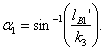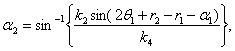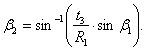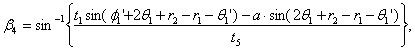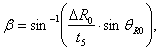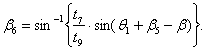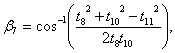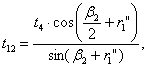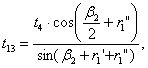Fundamentals and Practices of Sensing Technologies

by Dr. Keiji Taniguchi, Hon. Professor of Engineering

University of Fukui, Fukui, Japan

Xi’ an University of Technology, Xi’ an, China

Dr. Masahiro Ueda, Honorary Professor, Faculty of Education and Regional Studies

 University of Fukui, Fukui, Japan

Dr. Ningfeng Zeng, an Engineer of Sysmex Corporation

(A Global Medical Instrument Corporation), Kobe, Japan

Dr. Kazuhiko Ishikawa, Assistant Professor

Faculty of Education and Regional Studies, University of Fukui, Fukui, Japan

 

[Editor’s Note: This paper is presented as Part XII of a series from the new book “Fundamentals and Practices of Sensing Technologies”; subsequent chapters will be featured in upcoming issues of this Journal.]

 

 

Chapter Five – Part IV

 

5.11 Thickness Sensor for Glass Bottle

 

5.11.1 Introduction

 

Despite the emergence of plastics in the last half-century, bottles are still widely used as vessels for containing liquids. Recently, bottles of minimum thickness have been manufactured in order to lighten the weight for ease of conveyance, minimize the cost of their production, and save resources. However, bottles must be manufactured in such a way as to prevent their breakage during conveyance and use. Breakage is often due to a lack of uniformity in the bottle's thickness. Thus, a real-time and non-contact method for measuring bottle thickness is required for their systematic mass production.

For this purpose, some non-destructive methods have been developed using light^43)~47), including our method^45)~47). The method using ultrasound has generally poor resolution in thickness measurement. The method using radioisotopes has higher resolution, but this method is rather expensive to employ systematically.

An optical system is usually easy to construct and has sufficient resolution for practical use. However, the methods described in the Ref.⁴³⁾ depend on laser-light interference, and thus cannot be used in on-line measurement due to vibration. The method described in the Ref.⁴⁴⁾ measures bottle thickness directly based on the reflection method, which is employed in our method as a supplementary method for the determination of the bottle center. The reflection method usually has higher sensitivity; however, it can only be applied to a mirror-like surface because the reflected light must be received clearly on the CCD array⁴⁷⁾. Since the surface of a bottle is often rough, the practical application of this method is limited. Further, the surface requires a uniform inclination so that the reflected light can be captured on a relatively small CCD array. The image method, as opposed to the reflection method, can easily be used on rough surfaces and avoid such requirements.

The previous methods^43),44) produce some measurement errors in practical use due to the bottle's vibration, i.e., the dislocation of a bottle center, caused by on-line measurement. This dislocation causes a change of the incident angle of the laser light on the surface, which causes a measurement error and prevents the practical use of such systems. In this section, we propose a simple and ingenious system for accurately measuring bottle thickness; the proposed system combines the image method and the reflection method and produces no measurement error, making it feasible for successful employment in practical contexts^45),46).

 

5.11.2 Principle and Method

 

A. Outline of the Method

 

This method uses both reflected and scattered lights on the bottle surface and is based on the diffraction of these lights at each boundary. Figure 5.57 shows the optical principle for this method. The scattered light on both the outer and inner surfaces of the bottle is focused onto a CCD array by means of both lenses, as shown in Fig. 5.57(a): we call this "the image method". On the other hand, the reflected light on both the outer and inner surfaces of the bottle reaches the CCD array directly as shown in Fig. 5.57(b): we call this "the reflection method". Both image and reflection methods have successfully been used for measuring surface displacement and surface roughness in our previous paper, where the optical basis has been described in detail⁴⁷⁾.

 

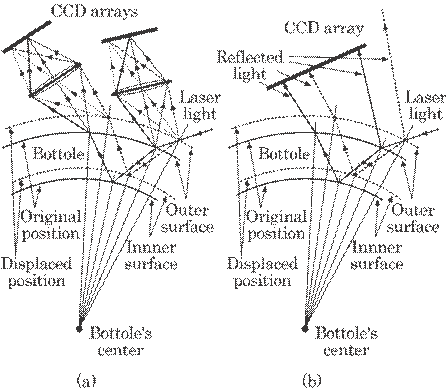
Fig. 5.57 Optical principle for this method: (a) for the image method, (b) for the reflection method.

 

 

The reflection method usually has higher sensitivity than the imaging method. It cannot, however, be applied to rough surfaces and surfaces with local curvature, because the reflected light on such a surface cannot be captured on the CCD array as shown by the dotted line in Fig. 5.57(b). By contrast, the image method shown in Fig. 5.57(a) can be successfully used in such situations. Thus, the technique in this paper is based fundamentally on the image method, with the reflection method used as a supplementary method to detect a dislocated bottle center as described in 5. 11. 2. C.

When an irradiated surface is dislocated mainly due to the change of bottle thickness and the dislocation of the bottle center, the surface and thus the image position on the CCD array changes, which makes it possible to measure the bottle thickness.

 

B. Analysis of Bottle Thickness under the Condition of a Fixed Center with Two Lenses

 

The image method is first analyzed using a fixed bottle center and only regarding the two-lens system. Figure 5.58 shows the optical principle for measuring bottle thickness. As

 

 

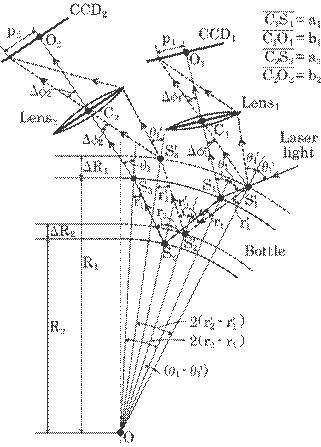
Fig. 5.58 Optical principle for measuring bottle thickness under the condition of a fixed bottle center.

 

 

described above, the thickness can be calculated by a light-ray tracing of the diffraction at each boundary. The optics are so arranged that the irradiation positions S₁ and S₃, corresponding to S₂ for the standard thickness and O for the fixed center position, are imaged on the origins of both CCD arrays, O₁ and O₂. When both surfaces are dislocated slightly due to the change of thickness, these two image positions shift p₁ and p₂ from their origins. The thickness can then be determined by means of these shifts, p₁ and p₂, as follows (details are described in Appendix A):

 

(5.48)

 

where R₁ is the outer radius of the bottle and R₂ the inner radius. In this equation, a small change in the thickness of the outer radius, R₁, is given by Eq. (A. 1), sin r₁' by Eq. (A. 3), and sin r₂' by Eq. (A. 4), which are described in Appendix A.

Bottles are usually manufactured using a mould, thus ensuring that the outer radius R₁ will be constant. Therefore, the changes in thickness originate mainly from changes in the inner radius when the bottle center is not displaced at every measurement, as in this case. Here we can put R₁=0 in the above equations: this assumption is also used in the next analysis in section 5. 11. 2 C.

 

C. Analysis of Bottle Thickness Under the Condition of a Displaced Center with One Lens

 

The analysis described in section 5. 11. 2 B under the condition of a fixed center is not, however, practical, because the bottle's center is dislocated in practically every measurement, which leads to measurement error. In this section, it is shown how both reflection and image methods are used for measuring bottle thickness under the condition where the bottle center is dislocated. Thus, this method essentially eliminates measurement error.

Figure 5.59 shows the optical principle for measuring bottle thickness under the condition of a dislocated center. Scattered and reflected light are, in a practical sense, detected at different directions from each other by means of a half-mirror between the surface and a focusing lens, as shown in Fig. 5.59(c); the scattered light is detected on the CCD_A array and the reflected light on the CCD_B array. However, it is clear from Figs. 5.59(a) and (b) that the reflected light is also detected in the same direction as the scattered light, as if the half mirror does not exist, for the convenience of analysis. In these figures, the solid lines depict reflected and scattered light rays from the surface without center dislocation and the broken lines depict the rays from a surface displaced by center dislocation.

The position of the bottle center is analyzed by means of the position of both the reflected light on the CCD_B array and the imaged light on the CCD_A array. The shift amount R₀ and its direction _R0 are calculated as follows (details in Appendix B):

 

	(5.49-1)
	(5.49-2)

 

 

 

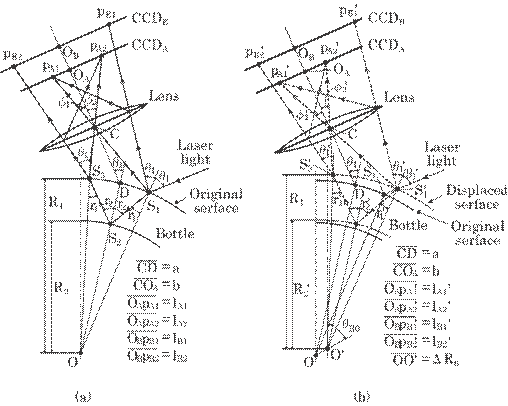
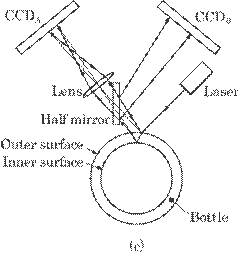
Fig. 5.59 Optical principle for measuring bottle thickness under the condition of a displaced center: (a) without center dislocation, and (b) with center dislocation. (c) outline of both scattered and reflected light rays.

 

where, ₁', which is the incident angle on a displaced surface, is given by Eq. (B. 3); k₁ is given by Eq. (B. 1) and ; k₂ by Eq. (B. 2), as described in Appendix B.

As described in 5. 11. 2. B, the outer radius is assumed to be practically constant, and any change of thickness can then be determined by means of the inner radius R₂', which is distinguished from R₂ in section 5. 11. 2. B. The inner radius, R₂', for this center position can then be calculated as follows (details in Appendix C):

 

(5.50)

 

where t₁₂ is given by Eq. (C. 3), t₁₄ by Eq. (C. 4), ₂ by Eq. (C. 1), and r₁'' by Eq. (C. 2), as described in Appendix C.

 

5.11.3 Results and Discussions

 

A. Practical System

 

Figure 5.60 shows the schema of our practical system for measuring bottle thickness under the condition of a dislocated center by a combination of the image and reflection methods. The system is composed of two main subsystems, i.e., the data processing

 

 

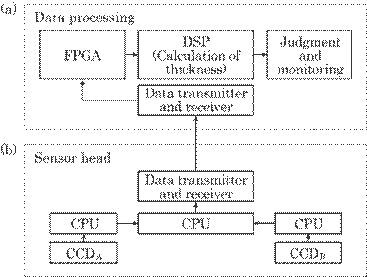
Fig. 5.60 Block diagram of this system for measuring bottle thickness under the condition of a displaced center by means of both image and reflection methods, (a) for the data-processing subsystem, and (b) for the sensor head.

 

 

subsystem shown in Fig. 5.60(a) and the sensor head shown in Fig. 5.60(b). The data obtained by both CCD arrays are A/D converted and amplified by means of an A/D converter. The data acquisition and data transmission are controlled by means of the CPU. Such data lead to a FPGA (field programmable gate array), and then to a DSP (digital signal processor) through a data transmitter and receiver. This DSP is the interface for fast-signal transmission with low-voltage differential signaling. The data are processed at the DSP, and the results including judgment of the bottle's acceptability are displayed on a monitor.

Both the scattered and reflected light from the outer and inner surfaces is received on the CCD_A and CCD_B arrays. The scattered light is focused onto the CCD_A array by a focusing lens. The reflected light is, however, defocused on the CCD_A due to the focusing lens, and is evenly distributed on this array. Thus, the image of the scattered light is clearly detected. On the other hand, reflected light from both surfaces is received on the CCD_B array by a half mirror placed between the bottle and the lens. The scattered light spreads widely and is evenly distributed over this array. Thus, only the reflected light can be clearly detected on CCD_B array. This scheme is mainly used to calculate the bottle's center. In conclusion, an image point on the CCD_A array and the reflection direction, i.e., a position on the CCD_B array, are clearly detected by this separation of the two kinds of light.

The measurement frequency of this system depends on the data acquisition speed of the CCD array and the data-processing speed. A data-processing speed which is between a few tens and a few hundreds kHz is sufficiently high. Then, the measurement frequency depends on the data-acquisition speed of the CCD array: CCD arrays with the speed of a few kHz are now on the market. Some measurements, usually a few tens measurements, are smoothed to obtain an accurate result because each signal will have a noise due to vibration caused by on-line measurement²⁹⁾. Thus the measurement frequency is finally a few hundreds of Hz, which is sufficient for practical use.

 

B. Resolution by Means of Simulation Experiment

 

A simulation experiment was performed using the computer software "Zemax^(r)", which is widely used for calculating optical paths, to estimate several optical characteristics: resolution, focusing characteristics, etc. This method is essentially based on the diffraction at the boundary. Figure 5.61 shows the optical arrangement in the simulation. The incident angle is determined for the bottle top as shown in this figure, and thus is not the same as that found on a normal surface.

 

 

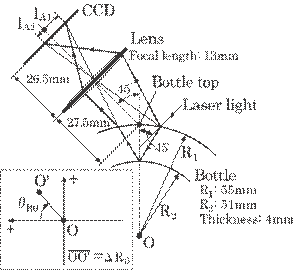
Fig. 5.61 Optical arrangement for a simulation experiment by means of the computer software "Zemax^(r)".

 

 

Table 5.6 shows the position detected on the CCD array for an optical arrangement involving combinations of different incident angles and dislocations. The resolution R_res, i.e., the smallest detectable difference of the thickness, can then be determined by means of the change of bottle thickness R, the change of irradiation position on the CCD array d and the resolution D_res of this CCD array as follows:

 

(5.51)

 

This resolution varies depending on the optical arrangement, such as incident angle , the magnification of the imaging optics, the position of the bottle center and the bottle thickness.

Table 5.7 shows the resolution obtained from the data in Table 5.6. The mean resolution for this arrangement was between 10 and 50 m, which is sufficient for practical application since the allowable maximum error for this purpose is about 0.1 mm. A smaller incident angle and lower magnification increase the value of R_res, since in this case the change of irradiation position, d, becomes smaller for the same value of R.

 

 

 

 

 

Table 5.6 Irradiation position in mm on the CCD array by the optical arrangement in Fig. 5.61 using the computer software "Zemax^(r)", (a) for l_A1, and (b) for l_A2.

 

 

 

Table 5.7  Resolution in m obtained by the optical arrangement shown in Fig. 5. (a) Result obtained by the scattered light on the inner surface with a small decrease in bottle thickness of -0.1 mm by changing the original inner radius from R₂=51 mm to 51.1 mm. (b) Result obtained by the scattered light on the inner surface with a small increase in bottle thickness of 0.1 mm by changing the original inner radius from R₂=51 mm to 50.9 mm. (c) Result obtained by the scattered light on the outer surface with a small decrease in bottle thickness of -0.1 mm by changing the original outer radius from R₂=55 mm to 54.9 mm. (d) Result obtained by the scattered light on the inner surface with a small decrease in bottle thickness of -0.1 mm by changing the original outer radius from R₂=55 mm to 54.9 mm. (e) Result obtained by the scattered light on the outer surface with a small increase in bottle thickness of 0.1 mm by changing the original outer radius from R₂=55 mm to 55.1 mm. (f) Result obtained by the scattered light on the inner surface with a small increase in bottle thickness of 0.1 mm by changing the original outer radius from R₂=55 mm to 55.1 mm.

 

 

 

 

In conclusions, the following results were obtained.

 

(1) The system consists of two main subsystems: one is a sensor head consisting of a laser as a light source, two CCD arrays for detecting the position of both reflected and scattered light and a focusing lens to image the light scattered on the CCD array, and the other is a data-processing subsystem consisting of a personal computer with an A/D converter and amplifier, and a monitor for displaying a thickness.

(2) The resolution of this method, i,e., the smallest measurable change in thickness, was between 10 and 50m for a CCD array with a pixel size of 10 m. This resolution is sufficient for practical applications. The measurement frequency of this system is about a few hundreds of Hz for a few tens of data smoothing. This is also sufficient for a practical use.

 

 

Appendix A

 

A small change in bottle thickness, R₂~R₁, in the case of a fixed bottle center, is derived by the following procedure. Some sectional details in this appendix are based on those shown in Fig. 5.58.

First, the small change in the outer radius, R₁, and the change in the incident angle from ₁ to ₁' due to change of bottle thickness, are calculated by means of the law of cosines and sines for the triangle S₁OS₁' as follows. Denoting the distance between S₁ and S₁' by , we obtain the following relation for R₁, from the law of cosines:

 

 

The small change of the outer radius, R₁, can, then, be obtained as follows:

 

(A.1)

 

where

 

 

which can be obtained by means of the law of sines for the triangle C₁S₁S₁' in Fig. 5.58. Further, we obtain the following relation for sin₁' by means of the law of sines for the triangle S₁OS₁' :

 

 

which leads to the following relation by means of (A. 1):

 

 

Next, we obtain the following relation for ₁ and sin by means of the law of cosines and law of sines for the triangle C₂OS₃' and C₂OS₃:

 

and,

 

where ₁ is the distance between C₂ and O, , and  the angle between OC₂S₃. Then, the following relation for sin  corresponding to the angle OS₃'C₂, can be obtained by referring to triangle C₂OS₃':

 

which leads to a following relation:

 

 

where

 

 

as shown in Fig. 5.58.

Finally, we obtain the relation for R₂ by means of the law of sines for a triangle OS₁'S₂':

 

 

which leads to:

 

(A.2)

 

where

 

	(A.3)
	(A.4)

 

and r₂ can be obtained as in appendix B.

 

 

 

Appendix B

 

The dislocated center position of the bottle, R₀ and R₀, can be analyzed by means of the sectional details shown in Fig. 5.62, which are based on Fig. 5.59(b).

 

 

Fig. 5.62 Sectional details for light rays at each boundary to detect the position of the

displaced bottle center, R₀ and_R0.

 

 

The angle ₁' in Fig. 3(b) is obtained experimentally as follows:

 

 

The angle r₂ in Fig. 3(a) is obtained from the law of sines for triangle OS₃S₂ as follows:

 

 

The distance  in Fig.5.62, denoted by k₁, is obtained by means of the law of sines for triangle DOD':

 

(B.1)

 

The distance , denoted by k₂, is also obtained by means of the laws of sines for triangle

CD'S₁':

 

(B.2)

 

Likewise, the distance , denoted by k₃, is given by

 

 

The angle ₁=O_BD'P_B1' can then be expressed by means of k₃ and l_B1', which is obtained experimentally:

 

 

Then by means of these values, the distance , denoted by k₄, is calculated using the law of cosines for triangle P_B1'D' S₁':

 

 

The angle ₂=D'P_B1'S₁' is then obtained by means of the law of sines for this triangle as follows:

 

 

Angle ₁' is expressed as follows:

 

(B.3)

 

The center dislocation R₀ and _R0 as expressed by Eqs. (2a) and (2b) in the text can be obtained finally by means of the law of cosines for triangle S₁OO' and the law of sines for this triangle.

 

 

 

Appendix C

 

In this appendix, the inner radius R₂', which ultimately provides the bottle thickness, is derived for the dislocated center position. Some distances t₁~t₁₁, and angles , ,  and  are defined as those in Fig. 5.62 and Fig. 5.63(a). The distance , denoted by t₁, is obtained by means of the law of sines for triangle CD'S₁' as follows:

 

 

where the angle ₂' is obtained experimentally by

 

 

 

 

 

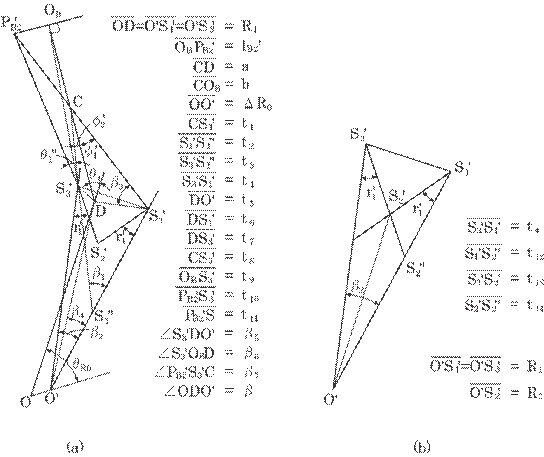
Fig. 5.63 Sectional details for light rays at each boundary to obtain the inner radius R2': (a) for the calculation of t1~t11, and angles , ,  and , (b) for the calculation of t₁₂~t₁₄ and R₂'.

 

 

Angle ₁ can then be obtained as follows:

 

 

The distance , denoted by t₂, can then be calculated by means of the law of cosines for triangle CS₁''S₁':

 

 

Similarly, the distance , denoted by t₃, can be calculated by means of the law of cosines for triangle S₃'O'S₁'':

 

 

The angle ₂ is then obtained by means of the law of sines for this triangle as follows:

 

(C.1)

 

The distance , denoted by t₄, can be calculated by means of the law of cosines for triangle S₃'O'S₁',

 

 

The distance , denoted by t₅, can also be calculated by means of the law of cosines for triangle DOO':

 

 

Using these values, the angle ₄ and the distance , denoted by t₆, can be obtained by means of the laws of sines and cosines for triangle DO'S₁':

 

 

Then the distance , denoted by t₇, can also be calculated by the law of cosines for triangle S₃'O'D:

 

 

from which, the angle ₅ is obtained by means of the law of sines for this triangle:

 

 

The small angle , which is caused by a center dislocation, is obtained by means of the law of sines for triangle ODO':

 

 

from which the angle S₃'DC is given by:

 

 

The distance  denoted by t₈, is then calculated by means of the law of sines for triangle CS₃'D:

 

 

The distance  denoted by t₉, and the angle ₆ can also be calculated by means of the laws of cosines and sines for triangle O_BS₃'D:

 

 

The distance  denoted by t₁₀, can then be calculated by means of the law of cosines for triangle O_BP_B2'S₃':

 

 

Further, the distance  denoted by t₁₁, can also be calculated by means of the law of cosines for triangle O_BP_B2'C:

 

 

The angle ₇, can be obtained by means of the law of cosines for triangle P_B2'S₃'C:

 

 

where,

 

(C.2)

 

We then calculate some values required for the calculation of R₂' by means of Fig. 5.63(b).

The distance , denoted by t₁₂, can be calculated by means of the law of sines for triangle S₃'S₂''S₁':

 

(C.3)

 

The distance , denoted by t₁₃, can also be calculated by means of the law of sines for triangle S₃'S₂'S₁':

 

 

Further, the distance , denoted by t₁₄, is calculated by means of the law of cosines for triangle S₁'S₂'S₂'':

 

(C.4)

 

Using the above obtained values, the inner radius R₂' can finally be given by Eq. (5.50) in the text by means of the law of cosines for triangle S₂'OS₂''.

 

 

 

5.12 Thickness Sensor for Film

 

5.12.1 Introduction

 

Thin films, for an example a lap film, and thin coatings, for examples an insulating vanish and a ceramic coating, have recently seen increasing use in many industries such as semiconductor and IC industries, the packaging industry, and the automobile industry. In these cases, accurate and real-time measurement of the thickness of coatings and films is very important for determining durability and cost performance. Many methods using light have been developed and realized^48)~50). These methods are based on laser light interferometry and have high accuracy. However, they were not real time measurement, and further expensive.

In addition to these methods, we have proposed an optical method using laser interference at many incident angles for direct measuring of the thickness of a thin film or a coating.⁵¹⁾ However, this method could not measure the film thickness in real-time since the method required a movable mechanism to allow variations in the incident angle. We then improved the method so as to measure thickness in real-time by means of a sheet laser light and a CCD array sensor.^52),53) This method was based on a time smoothing of many reflected lights from slightly different irradiation positions. Thus, the method can measure thickness roughly in real time.

In this section, a practical system for measuring film thickness essentially in real time has been devised which involves a laminar-like laser light and a CCD camera. The system's performance is also discussed.⁵⁴⁾

 

5.12.2 Principle and Method

 

A. Previous Method Using a Sheet Laser Light

 

The basic principle of this method depends on a multi-wave laser interference of both light reflected on the upper and lower surfaces of the coating, as was shown in the previous paper⁵¹⁾. The reflective power of both surfaces affects only a contrast of the interfered light intensity and does not affect measurement errors of the thickness. An outline of the previous method using a sheet laser light is described in detail in this section. Figure 5.64 expresses the basic principle of this method. The basic optical arrangement consists of a laser, a collimator (not shown in this figure), two cylindrical lenses, and a photo-receiver. A sheet laser light is focused on the film as a point illuminator and is reflected onto a photo-receiver array. As is shown in this figure, each small portion of the sheet laser light is received on a corresponding small portion of the photo-receiver array such as  to ', and  to '.

 

 

 

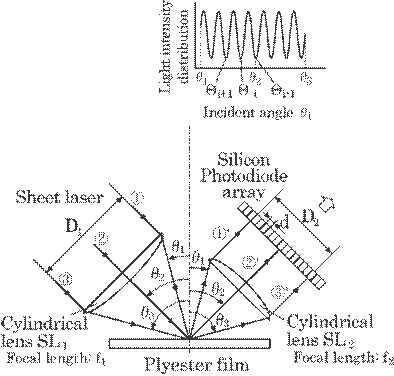
Fig. 5.64 Basic optical arrangement for measuring film thickness by means of laser interferometry.

 

This eliminates the need of a mechanism for varying the incident angles as required for the previous method.⁵¹⁾ The spatial resolution of incident angle, _m, is then determined by an element size of the photo-receiver array, d, and a focal length of the cylindrical lens SL₂, f₂, as follows:

 

(5.52)

 

The maximum variable range of the incident angle, (₃-₁)_max in this case, is given by whichever is the smaller of the two bellow:

 

or

(5.53)

 

where ₃ and ₁ are the maximum and minimum incident angles, D₁ and D₂ the effective size of both cylindrical lenses SL₁ and SL₂, and f₁ and f₂ the focal length of these lenses.

The reflected lights on both the upper and lower surfaces of the film interfere with each other and result in a sign-like intensity distribution R on the CCD array sensor as is shown in a cut in Fig. 5.64, which is a basis of this method. The thickness of the film, h, can be expressed as follows:⁵¹⁾

 

	(5.54)
	(5.55)

 

where _i expresses the incident angle where the light intensity distribution has minimum values, n a refractive index of the film, and _i+1<_i<_i-1, as shown in a cut in Figure 5.64. The above two equations are basically the same since each was derived from the same few equations.⁵⁵⁾ Theoretically, Eq. (5.55) does not require a known n, but it requires three consecutive , i.e., _i+1, _i, and _i-1, and further rather high accuracy in _i. On the contrary, Equation (5.54) requires only two consecutive , i.e., _i+1, _i,  but requires known n, and can be practically used for a known n.

 

B. Present Method by Means of Laminar-Like Laser Light

 

The above description was a basic principle of this method, which uses a sheet laser light. The largest problem involved in this method was a large fluctuation in the light intensity distribution on the photo-receiver array, which makes an accurate determination of _i difficult.⁵¹⁾ However, this problem can be solved by means of the smoothing of many data. Two methods are considered for this smoothing: one is time smoothing, and another is spatial smoothing. Time smoothing was achieved in the previous method by means of a sheet laser light⁵¹⁾, which requires a slight shift of the film. This prevents this method from measuring the thickness of a layer essentially in real time.

The method was further improved so as to measure the film thickness essentially in real time by means of a laminar-like laser light. Figure 5.65 expresses the optics for this method, which uses spatial smoothing. The laminar-like laser light with a width W is focused onto a line on the film, and is reflected onto the cylindrical lens SL₂, which is received on the CCD camera with horizontal dimension D₂ and vertical dimension W. In the previous method, an irradiated position O on the film was slightly moved by shifting the film, and many light intensity distributions from these irradiated points were smoothed in time, i.e., time smoothing. On the contrary, many light intensity distributions arisen from line O'OO'' are recorded on a 2-D CCD camera by only one flash of laser light, and smoothed in space, i.e., spatial smoothing. This enables essentially real-time measurement, because the method does not require shifting of the film.

 

 

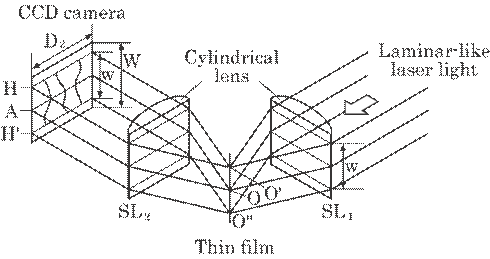
Fig. 5.65 Basic optics for measuring film thickness by means of laminar-like laser light.

 

C. Determination of _i

 

The method in this study requires only two or three successive incident angles _i for a determination of film thickness, as was shown in Eqs. (5.54) and (5.55).

Figure 5.66 shows an example of the interference pattern on the CCD camera, i,e., the light intensity distribution, to obtain spatial smoothing.²⁹⁾ The light intensity distribution on

 

 

Fig. 5.66 Interference pattern on the CCD camera for spatial smoothing.

 

 

each horizontal line is arisen from each corresponding position on a line O'OO'' on the film, and all the data on a line O'OO'' are recorded on the CCD camera. Each light intensity distribution can, basically, be used for the determination of _i.

However, the angle _i cannot be determined from this distribution, because it fluctuates considerably due to speckles inherent in laser light as is shown in Figure 5.67(a). Such fluctuation can, however, be decreased by smoothing many sampling data on the horizontal lines. The method of spatial smoothing is basically the same as that of time smoothing. Figure 5.67 shows this smoothing effect in space. Thus, the smoothing by N samples decreases the fluctuation remarkably; the fluctuation is linearly proportional to 1/, when the sampling data have usually a normal distribution.^29),30)

 

 

 

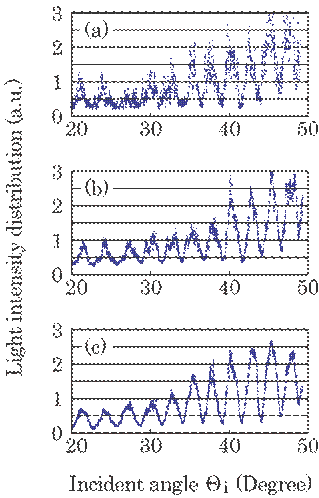
Fig. 5.67 Smoothing effect by means of the light intensity distribution on each horizontal line: (a) no smoothing, (b) smoothing by 10 samples, (c) smoothing by 50 samples.

 

 

5.12.3 Performance of the Practical System

 

A practical system was constructed. Figure 5.68 shows the appearance of this system, and Table 5.8 its main performance.

 

 

 

 

Fig. 5.68 Appearance of the system. (a) Top view, and (b) side view.

 

 

Table 5.8 Performance for this system.

 

 

 

 

The measurement frequency of a film thickness was determined mainly by the sample number for smoothing, N, and the speed of a 16 bit A/D converter in the processing circuit. The frequency was about 50 Hz, which is almost enough for practical use.

The measurable minimum thickness of the film is 2.4 m, and the maximum thickness is about 1.2 mm for the laser with a wavelength of 405 nm and the refractive index of a film of 1.4, which is discussed in section 5.12.4. The working distance between the sample and the system head is about 7 mm.

A variable range of incident angle, ₁~₃ in Figure 5.64, was limited to a rather small range of 12 from the optical axis inclined 45 in the horizontal direction from the consideration of measurement error due to the spherical aberration of both cylindrical lenses. This lowers the resolution of this optical system, in other words, increases the smallest measurable film thickness to about three times of the value obtained by the variable range of 0~90.⁵¹⁾ However, this small range of incident angle reduces the measurement error of the film thickness, as is discussed in 5.12.4.

 

5.12.4 Measurable Minimum and Maximum Film Thickness

 

Film thickness can be calculated by means of Eq. (5.54) or (5.55). Thus, two or three consecutive _i should exist between 4512 for this calculation. The pitch of the light intensity distribution, i.e., an angle between each _i, increases when the thickness diminishes, and two consecutive _i can't exist in this range of incident angle when the thickness becomes too small, as is shown in Fig. 5.69.

 

 

 

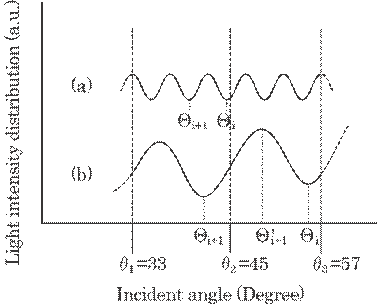
Fig. 5.69 Light intensity distribution for thick (a) and thin (b) films.

 

 

This determines the measurable minimum thickness h_min, in other words, the spatial resolution of this method, as follows;⁵¹⁾

 

(5.56)

 

where _1p is the practical minimum incident angle, and _3p the maximum incident angle, which are 33 (=45-12) and 57 (=45+12) for this practical system, respectively, as described above. Thus, the spatial resolution can be determined by the wavelength of the laser, the refractive index of the film, and the minimum and maximum incident angles. As an example, h_min5.9=2.4m can be obtained for =405 nm and n=1.4.

On the other hand, the measurable maximum thickness is determined by the spatial resolution of an incident angle , defined by

 

(5.57)

 

where d is the spatial resolution of the CCD camera in the horizontal direction, and f₂ the focal length of the cylindrical lens SL₂. In this system, the angle resolution was found to be =4.010^-4 for d=10 m and f₂=25 mm. Theoretically, one pitch of the light intensity distribution can be reproduced only by two sampling data as based on the sampling theory.³⁰⁾ Thus, it is practically sufficient to use ten sampling data for that reproduction. That is, the maximum measurable thickness h_max can be obtained when two consecutive minimum of the light intensity distribution exist within 10=4.010^-3=0.023. For example, h_max becomes 30201.22 mm by substituting _i+1=45.0and _i=45.023 into equation (5.54) for =405 nm and n=1.4.

 

In conclusions, the following results were obtained.

 

(1) The system consists of two main sub-systems; one is an optical system composed of a laser having a wavelength of 405 nm, two cylindrical lenses, and a CCD camera, and another is a data processing system.

(2) The main performance of this system is as follows, for a variable angle of incident light of 33~57, a laser wavelength of 405 nm, and a film refractive index of 1.4. The measuring frequency is about 50 Hz in standard use. The measurable minimum thickness is 2.4 m, and the maximum thickness is 1.2 mm. The working distance is 7 mm, which is sufficient for practical use.

 

 

References

 

43)  FE Irons: An interferometric measurement of the wall thickness of a cylindrical glass tube with application to a draining liquid film, Meas. Sci. Technol. 6-9(1995) 1356.

 

44)  T. Suzuki; Pat. : Devices for thickness measurement of glass bottle, Pat. (A) 11-190614 (1999) in Japan.

 

45)  M. Ueda, & T. Matsumoto: System for measuring glass thickness, Pat. Pen. 2005-348137 (2005) in Japan.

 

46)  Q. Shu, T. Kozuki, K. Ishikawa, T. Matsumoto, H. Suga, T. Sakurai, & M. Ueda: Real time measurement of a bottle thickness by means of both imaging and reflection methods, Rep. 344^th Topical Meet. Laser Soc. Jpn. RTM-06-01(2006) 1.

 

47)  M. Kawazu, K. Ishikawa, H. Suga, T. Sakurai, &  M. Ueda: Real time measurement of a bottle thickness by means of both image and reflection methods, Meas. Sci. Technol. 18(2007) p. 295.

 

 

 

48)  O. S. Heavens: Optical properties of the thin films, Dover, New York, 96(1991) p. 103.

 

49)  H. G. Tompkins, W. A. McGham: Spectroscopic ellipsometry, a use's guide, New York, Wiley-Interscience, (1990).

 

50)  C. Jung, B. K. Rhee: Simultaneous determination of thickness and optical constants of polymer thin film by analyzing transmittance, Appl. Opt., 41(2003) p. 3861.

 

51)  K. Ishikawa, H. Yamano, K. Kagawa, K. Asada, K. Iwata, & M. Ueda: Measurement of thickness of a thin film by means of laser interference at many incident angles, Opt. Laser Engr., 41-1(2004) p. 19.

 

52)  K. Ishikawa, H. Yamano, K. Kagawa, K. Asada, k. Iwata, & M. Ueda: Real-time measurement of a thickness of a thin coating by means of sheet laser, Opt. Lasers Engr.: 41-1(2004) p. 731.

 

53)  K. Ishikawa, F. Murase, Z. Feng, & M. Ueda: Real-time measurement of a thickness of a thin coating by means of sheet laser, Rep. 308^th Topical Meeting, Laser Soc. Jpn. Laser Measurements, No. RTM-03-09(2003) p. 23.

 

54)  F. Zhu, K. Ishikawa, T. Ibe, & M. Ueda: A practical system for measuring film thickness, and some discussion, Rep. 320^th Topical Meeting, Laser Soc. Jpn. No. RTM-04-06(2004) p. 1.

 

55)       T. Tsuruta: Applied optics I and II: (1998) p. 33 ( in I) and p. 114 ( in II).

 

[The segment concludes Chapter 5; Chapter 6 will be presented in the upcoming March-April 2011 issue of this Journal.]