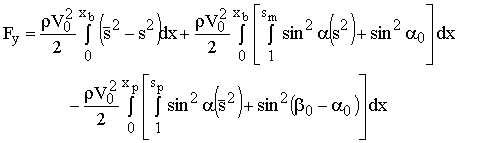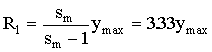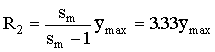Science: Physics:
|
|
Some Notes on Power Interaction Between Viscous Flow
and Some Profiles with Forward Sharp Edge
By
Dr. Alexander B. Shandyba
Sumy State University, Ukraine
ABSTRACT: This paper deals with the contraction/expansion phenomenon in viscous flow under streamlining of bodies. The use of simple hydraulic methods and early proposals [1-4] serves to decompose the problem.
1.
INTRODUCTION
It is widely accepted that the external streamlining problem may be solved with the analytic functions, ideal fluid and viscous boundary layer theories as well as the virtual mass and bound vortex models. At the same time, the bound vortex model (Kutta-Joukowski) supposes that a finite velocity exists at the back sharp edge but the forward edge must be smooth for passing boundary streams from the lower side of wing profile to the more convex upper side, according to the Magnus' phenomenon. Fixation of the separation point at the back sharp edge by the Joukowski-Chaplygin condition allows the circulation value to be found.
In the
case of a forward sharp edge, there is a blocking of the bound vortex and we
shall receive a lifting force of more than Newton's impulse component
correlated to ![]() as a function of attack angle. For example, lifting force
coefficient Cy and drag resistance coefficient Cx are
presented as the sum, in accordance with Betz and Fedyaewski works [1-4]:
as a function of attack angle. For example, lifting force
coefficient Cy and drag resistance coefficient Cx are
presented as the sum, in accordance with Betz and Fedyaewski works [1-4]:
|
|
(1) |
|
|
(2) |
![]()
where ![]() = attack angle;
= attack angle; ![]() = differential of lifting force coefficient;
= differential of lifting force coefficient; ![]() = constant of drag
resistance coefficient considered for this approach [4].
= constant of drag
resistance coefficient considered for this approach [4].
At the present time we have only limited evidence of development of these early proposals regarding power interaction.
2.
IMPULSE (NEWTON'S) COMPONENT OF INTERACTION
Having
received numerous experimental correlations of power interaction of
non-circulation separated flow under great angles of attack, we can see that
the prevailing share of impulse (Newton's) component into drag resistance and
lifting force [1-8]. So, drag resistance of struts, wires and building
long-ware inclined to the wind direction, depends on the ![]() function [7,8]. Yet
Eiffel's experiments with plates in air flow stated that the share of impulse
component of lifting force increases under lengthening plate along the wind
direction (fig.1). Perhaps, such an approach of the experimental curves to the
theoretical function can be explained by a decreasing influence of the unequal
conditions of streamlining and local attack angles of the boundary streams.
function [7,8]. Yet
Eiffel's experiments with plates in air flow stated that the share of impulse
component of lifting force increases under lengthening plate along the wind
direction (fig.1). Perhaps, such an approach of the experimental curves to the
theoretical function can be explained by a decreasing influence of the unequal
conditions of streamlining and local attack angles of the boundary streams.
Moreover,
for finding a "pure relationship", it was suggested to equip testing
plates with stream-forming longitudinal stabilizers and the upper
stream-separating edge (fig.2). By means of equal influence of local attack
angles and equal area of separation at such condition we could show a better
correspondence with theoretical ![]() function. On the
other hand, the lifting force of the plane long wing equipped only with the
upper stream-separating edge for the constant area of separation under great
angles of attack corresponds with this function too. We have shown the
confirmative results also in the previous paper [2]. To analyze the components
of aero-hydrodynamic forces it seems like a reasonable way to determine the
pure relationships without any shares of the accompanying factors or to take
them into account and to level their influence.
function. On the
other hand, the lifting force of the plane long wing equipped only with the
upper stream-separating edge for the constant area of separation under great
angles of attack corresponds with this function too. We have shown the
confirmative results also in the previous paper [2]. To analyze the components
of aero-hydrodynamic forces it seems like a reasonable way to determine the
pure relationships without any shares of the accompanying factors or to take
them into account and to level their influence.
3.
CALCULATION OF PROFILE INFLUENCE
To
evaluate a possibility and origin of lifting force for an endless segmentary wing
profile under attack angle ![]() we consider a typical
scheme (fig. 3). In this case the forward sharp edge divides the running flow
into two parts: upper and lower. Obviously, the upper part of flow undergoes
more intensive contraction by more convex side of the profile. The maximum
degree of contraction is observed near the maximum deviation of boundary
streams
we consider a typical
scheme (fig. 3). In this case the forward sharp edge divides the running flow
into two parts: upper and lower. Obviously, the upper part of flow undergoes
more intensive contraction by more convex side of the profile. The maximum
degree of contraction is observed near the maximum deviation of boundary
streams ![]() but after this we can
see an expansion of flow and some zone of separation. Contraction of the lower
part of flow is less intensive and the maximum comes at the back sharp edge
with the deviation
but after this we can
see an expansion of flow and some zone of separation. Contraction of the lower
part of flow is less intensive and the maximum comes at the back sharp edge
with the deviation ![]() .
.![]()
It
is necessary to note the connection between the internal streamlining and external
one is established with the influence radius. In fact, experimental data
indicate that we have the immutable flow at some midship diameter distance from
profile’s surface. There are immutable aero-hydrodynamic parameters (pressure,
velocity) out of the influence radiuses. Like the peculiar ring contraction
considered before in [2] also the 2D flow around profile can be imaged as two
2D contractions between the influence radiuses (R1 for lower side, R2 for upper side) and the head surface of the
profile. By this mean the external aero-hydrodynamics problem transforms into
the internal problem. Then solving can be found with simple hydraulic methods.
After
determination of the maximum contraction degree sm![]() it is possible to find the specific lifting force per unit
length by integrating the difference of pressures on the lower and upper sides:
it is possible to find the specific lifting force per unit
length by integrating the difference of pressures on the lower and upper sides:
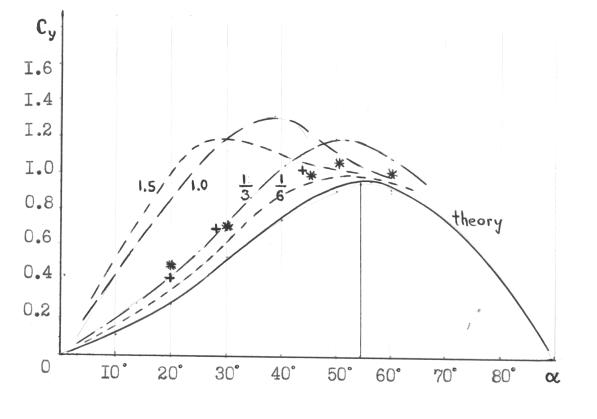
Fig.1 Approach of the
lifting force coefficients to the theoretical function:
---- curves 1.5 ; 1 ; 1/3; 1/6;
- Eiffel's experiments for different lengthening;
*** square plate with the
stream-forming equipment;
+++ plane wing with the
stream-separating edge.
stream-forming stabilizers
Fig 2. Square plate with the
stream-forming equipment.
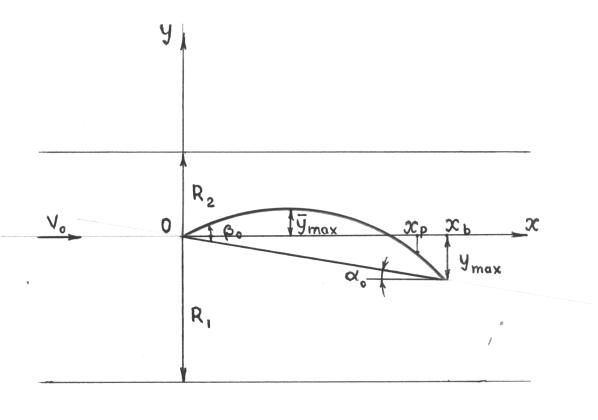
Fig.3 Scheme of profile influence.
|
|
(3) |
where 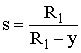 = current contraction degree on the lower
side;
= current contraction degree on the lower
side;
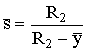 = current contraction degree on the upper
side;
= current contraction degree on the upper
side;
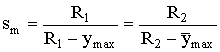 = maximum contraction degree;
= maximum contraction degree;
![]() = contraction degree at the separation point;
= contraction degree at the separation point;
![]() = current attack (contraction/expansion)
angle;
= current attack (contraction/expansion)
angle;
![]()
![]() = contraction
condition.
= contraction
condition.
According
to the presented model with the fixed maximum contraction degree, the influence
radii are the constants defined by the maximum deviations of the boundary
streams. The experimental data provide the reasons to suppose sm = 1.43 [2]. Consequently, the influence radiuses
will exceed the maximum deviations by 3.33 times:
|
|
(4) |
|
|
(5) |
A
position of the separation point on the upper side may be found by analysis of
the energy balance of boundary streams under the energy accumulation when ![]() and the energy
deliverance when
and the energy
deliverance when![]() . But this supposition needs to be accompanied with
representative experimental data.
. But this supposition needs to be accompanied with
representative experimental data.
4.
CONCLUDING REMARKS
-
Asymmetric
contraction /expansion phenomenon under asymmetric streamlining of bodies with
forward sharp edge results in generation of the profile components of lifting
force and drag resistance;
- The better agreement between the
experimental data and the theoretical lifting force curve for impulse Newton’s component
has been obtained with the auxiliary stream-forming equipment of the testing
plate;
- In order to provide adequate experimental
relations for influence of general attack angle, profile shape and contraction
degree it is necessary to take into account the local changes of boundary streams trajectories and their local power
interactions with flow.
REFERENCES:
1.
Betz
A. Aerodynamics.- Oborongiz Publ., 1940, Moskow (transl. from
German).
2.
Shandyba
A.B. Hydraulic Resistance of Bodies in Water Flow.- BWW Journal, May-June issue
2002, N3, USA.
3.
Fedyaewski
K.K. Application of the circulation-separation theory for short wings and
steering rudders.- Ship building Publ., 1973, Leningrad (in Russian).
4.
Wienhardt
T. Uber Antriebsverteilung des einfachen
Rechteckflugels uber die Tiefe.- ZAMM, 1939, Bd.19, H5.
5.
Eiffel
G. La resistance de l’air.- ZFM, 1910,
N8.
6.
Lawrence
H. The Lift Distribution on Low Aspect Ratio Wings at Subsonic Speeds.- IAI,
1951, vol.18, N10.
7.
Thurston
A.P. The resistance of inclined struts in a uniform air current.- Aerodynam.
Journal, 1915, XIX, N7.
8.
Relf
E.F., Powell C.H. Tests on smooth and
stranded wires inclined to the wind direction.- ACA, 1916/17, Rep. N307.
9.
Numerical
Methods in Fluid Dynamics, 1978, Editors: Wirtz H.J., Smolderen J.J. - von
Karman Institute of Fluid Dynamics, Rhode-Genese, Belgium.- Hemisphere Publ.
Dr. Alexander Shandyba is Assistant Professor of Safety Vital Activity at Sumy State University and heads a research group at New Technology Institute. He has devised numerous projects and is the author of 60 technical papers and inventions (see Hydraulic Resistance of Bodies in Water Flow, May-June 2002 issue of this Journal). Dr. Shandyba is also a Member of the publishing board of the Mechanical Engineering Journal.
[ BWW Society Home Page ]
© 2002 The BWW Society/The Institute for the Advancement of Positive Global Solutions