|
Abstract:
When low-energy photons fall on the material, there are three basic interactions that occur: the phenomenon of photoelectric absorption, Compton scattering, and Rayleigh scattering. Each of these interactions leads to a weakening of the incident ray by means of a complete loss of these photons by the photoelectric absorption, or losing part of its energy by means of Compton scattering, or scattering without loss of energy by means of Rayleigh scattering. In this paper, the phenomenon of photoelectric absorption, Compton scattering and Rayleigh scattering are introduced and discussed.
1. Introduction
To study the interaction of photons with matter, an understanding of the structure of these particles as well as their physical properties are in demand. The processes of photons absorption, Compton scattering and Rayleigh scattering can be described and explained in terms of interactions between particles. Particles in the beam of radiation (photons) strike particles in the material (electrons) and are either scattered or stopped. The photoelectric absorption, Compton scattering, and Rayleigh scattering actually describe three important photon interactions with matter at low energy which have wide uses [1-6]. They have application in solid state physics research, in medical diagnostic, in geology survey and exploring and in making biological shielding against hazards radiation. It was therefore thought to be of interest to introduce and discuss these processes so that those working in the field of research can acquire knowledge and benefit from it.
2. The Photoelectric Absorption
Photoelectric absorptions mainly occur with electrons that are strongly bound to the atom. Photoelectric absorptions are most likely foreseeable when the incident photons have higher energy than the electron’s binding energy. If the binding energy is higher than the energy of the photon, photoelectric absorptions cannot take place. It can be concluded that the mechanism of photoelectric absorptions is achievable only when the incident photon has enough energy to dominate the electron’s binding energy and remove the electron from the atom [1-5]. The photoelectric absorption cross section is proportional to the atomic number of the material and inversely to incident photon energy and is given as [1,2]
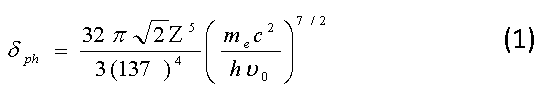
Where Z is the atomic number, me is the electron mass, c is the speed of light and hʋ0 is the incident photon energy. It can be seen from equation 1, that the photoelectric absorption cross section is proportional to the atomic number of the material and inversely to incident photon energy.
Figure 1 shows the photoelectric absorption cross sections of lead, iron and aluminum in terms of the energy of the incident photon.
Figure1: The photoelectric absorption cross sections of (a) lead, iron and aluminum and (b) muscle, bone and water in terms of the energy of the incident photon
3. Compton Scattering
Compton scattering is a process in which only a portion of the incident photon energy is transferred to the atomic electron and the photon is scattered in different direction with reduced energy [7-14]. Figure2. shows a schematic diagram describing the mechanism of Compton scattering.
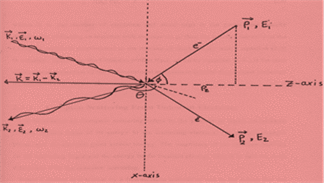
Figure2: Schematic diagram describing the Compton scattering interaction between an incident photon with initial wave vector k1, energy ω1, unit polarization ε1 and an electron with initial momentum P1 and energy E1. The photon scatters at scattering angle Ө with wave vector k2, energy ω2, unit polarization ε2 and the electron recoils with momentum P2 and energy E2 [11].
By combining the laws of energy and momentum conservations and studying the details of the collision, Compton found a relationship between the change in the wavelength of the scattered photon and the angle of scattering, which is completely consistent with the experiments. This is the known Compton equation [1, 2].
![]() (2)
(2)
Where λ1 and λ2 are the wavelength of the incident and scattered photon respectively. θ is the scattering angle, h is plank constant, m is the electron mass and c is the speed of light. Equation (2) can be rewritten in terms of the energy of incident and scattered photon as:
![]() (3)
(3)
Where ω1 and ω2 are the energy of the incident and scattered photon respectively. This equation emphasizes the fact that the change in the energy of a scattered photon depends strongly on the energy of the incident photon. Compton scattering means a process in which an incident photon transfers some of its energy to atomic electron. A photon changes its phase and the electron acquires kinetic energy. The amount of change in the energy of the scattered photon depends on the scattering angle and the energy of the incident photon. When a photon is scattered with the free and static electron, this means that the atomic bonding energy can be neglected compared to the high energy transferred to the electron by the incident photon. On this basis, collision can be described by the laws of energy and momentum conservations and differential scattering of the cross-section can be predicted with good accuracy by klein – Nishina cross section for unpolarized photons as [1-5].
![]() (4)
(4)
Where r0 is classical electron radius, θ is the scattering angle and ω1 and ω2 are the energy of the incident and scattered photon respectively. However, electrons are bound to the atoms. Therefore, Compton scattering by bound electrons requires taking into account the electron binding energy (see [11]). As a result, the Compton scattering cross-section can theoretically be calculated with the following relationship:
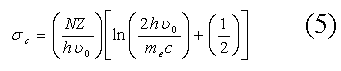
Table1 shows the calculated Compton scattering cross sections for lead, iron,
aluminum, muscle, bone and water in terms of the incident photon
energy (10-150 keV). Data of table1 are plotted in figure3.
Table1 presents the calculated Compton scattering cross sections for lead, iron, aluminum, muscle, bone and water in terms of the energy of the incident photon
|
(cm2/g) |
photon
energy keV |
||||||
|
Muscle |
Bone |
Water |
Pb ,
z=82 |
Fe ,
z=26 |
Al ,
z=13 |
|
|
|
0.212 |
0.205 |
0.214 |
0.1526175 |
0.180026 |
0.1857024 |
10 |
|
|
0.208 |
0.201 |
0.21 |
0.1500012 |
0.175714 |
0.1823544 |
15 |
|
|
0.205 |
0.197 |
0.207 |
0.1473849 |
0.173558 |
0.1792296 |
20 |
|
|
0.198 |
0.191 |
0.20 |
0.142443 |
0.16709 |
0.1734264 |
30 |
|
|
0.192 |
0.185 |
0.193 |
0.1380825 |
0.1617 |
0.1678464 |
40 |
|
|
0.186 |
0.179 |
0.188 |
0.133722 |
0.157388 |
0.162936 |
50 |
|
|
0.181 |
0.174 |
0.182 |
0.1299429 |
0.15076 |
0.1582488 |
60 |
|
|
0.171 |
0.165 |
0.173 |
0.1232568 |
0.144452 |
0.1499904 |
80 |
|
|
0.163 |
0.157 |
0.165 |
0.1174428 |
0.137984 |
0.1430712 |
100 |
|
|
0.147 |
0.142 |
0.148 |
0.1058148 |
0.12397 |
0.1287864 |
150 |
|
(a) (b)


Figure3 shows the Compton scattering cross sections for (a) lead, iron and aluminum and (b) for muscle, bone and water in terms of the energy of the incident photon
4. Rayleigh scattering
Rayleigh scattering is an elastic scattering since the photon energies of the scattered photons is not changed. It results from the electric polarizability of the particles. The oscillating electric field of the incident photons acts on the atomic electrons, causing them to move at the same oscillating frequency. The atomic electrons, therefore, become small radiating dipoles whose emitting radiation is seen as scattered photons with the same energy as the energy of the incident photons. In general, we find that the Rayleigh cross-section is proportional to the square of the atomic number of the material and inversely proportional to the energy of the incident photon and can be expressed as [1]:
![]() (6)
(6)
Table2 shows the calculated Rayleigh scattering cross sections for lead, iron, aluminum, muscle, bone and water in terms of the incident photon energy (10-150 keV). Data of table 2 are plotted in figure4.
Table2 presents the calculated Rayleigh scattering cross sections for lead, iron,
aluminum, muscle, bone and water in terms of the energy of the incident photon
|
|
photon energy kev |
|||||
|
Muscle |
Bone |
Water |
Pb , Z=82 |
Fe , Z=26 |
Al , Z=13 |
|
|
0.177 |
0.285 |
0.183 |
4.8764925 |
1.145914 |
0.4928256 |
10 |
|
0.097 |
0.166 |
0.099 |
3.1930488 |
0.692076 |
0.2707416 |
15 |
|
0.061 |
0.108 |
0.063 |
2.2276341 |
0.471086 |
0.1711944 |
20 |
|
0.031 |
0.055 |
0.032 |
1.284894 |
0.252252 |
0.0877176 |
30 |
|
0.018 |
0.033 |
0.02 |
0.8386695 |
0.155232 |
0.0528984 |
40 |
|
0.012 |
0.023 |
0.012 |
0.587214 |
0.104566 |
0.0352656 |
50 |
|
0.009 |
0.016 |
0.009 |
0.4340151 |
0.07546 |
0.0252216 |
60 |
|
0.005 |
0.01 |
0.005 |
0.2604672 |
0.045276 |
0.0147312 |
80 |
|
0.004 |
0.006 |
0.003 |
0.1712223 |
0.028028 |
0.0093744 |
100 |
|
0.002 |
0.003 |
0.002 |
0.0799425 |
0.012936 |
0.0042408 |
150 |
.
(a) (b)


Figure4 shows the Rayleigh scattering cross sections for (a) lead, iron and aluminum and (b) for muscle, bone and water in terms of the energy of the incident photon
5. The biological Shielding
The danger of dealing with x-ray or radioactive sources lies in the high penetration power of each of the rays, and therefore all preventive precautions must be taken into account when dealing with x-ray or radioactive sources, because their effect on the human body leads to the destruction of live cells and unexpected chemical changes in the human body. In addition, they may cause serious diseases that do not appear until several years after exposure to these rays. They also cause genetic changes that may appear in subsequent generations (rapidly dividing cells are destroyed at a much higher rate than stable cells).
Therefore, when dealing with x-rays and radioactive sources, it is necessary to know the extent of the effect of these rays on the materials in order to know the expected risk, and with this knowledge it is possible to extract some materials with useful properties for building protective barriers, "Shielding" that protect humans from the damages of these radiation as well as allow control over these radiation sources.
Table3 shows the calculated mass absorption coefficients for the elements lead, iron and aluminum in terms of the energy of the incident photon up to 150 keV. Data was plotted in figure5
Table 3: The calculated mass absorption coefficients for lead, iron and
aluminum in terms of the incident photon energy of the up to 150 keV.
|
Pd |
Fe |
Al |
Photon Energy ( keV ) |
|
Mass Absorption Coefficient |
|||
|
132.93711 |
172.72794 |
26.346528 |
10 |
|
114.97185 |
55.84579 |
7.930296 |
15 |
|
85.515219 |
25.546444 |
3.408264 |
20 |
|
29.515219 |
8.127042 |
1.120464 |
30 |
|
13.971042 |
3.61512 |
0.5667048 |
40 |
|
7.814016 |
1.943634 |
0.3689496 |
50 |
|
4.0866318 |
1.203048 |
0.280116 |
60 |
|
2.331414 |
0.595056 |
0.203352 |
80 |
|
1.4049851 |
0.369754 |
0.171306 |
100 |
|
1.0706553 |
0.1964116 |
0.13822776 |
150 |
The mass absorption coefficients for aluminum, iron and lead was calculated in terms of the incident photon energy. The first element represents light elements, the second represents medium elements and the third represents heavy elements

Figure5: shows the mass absorption coefficients for aluminum, iron and lead calculated in terms of the incident photon energy
When dealing with radioactive sources at energy (1MeV) and seeking to know the properties of natural materials to make protective barriers such as {Sand, Clay, Rubber, Cements, Kaolin}, which are characterized by their abundance and ease of obtaining them when necessary. These natural materials are available and can be used to make the necessary precautions. Table4 shows the calculated thicknesses (t) for Kaolin, Clay, Cement, Sand, Rubber, Lead and Tungsten for incident photons at 1MeV.
Table4: Shows the relationship between the thickness of materials and the
transmitted photon intensity when the incident photon energy is at 1MeV.
|
Tungsten t "
cm " |
Lead t "
cm " |
Rubber t "
cm " |
Sand t "
cm " |
Cement t "
cm " |
Clay t "
cm " |
Kaolin t"
cm " |
Transmitted intensity I |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0.08 |
0.12 |
1.6 |
0.75 |
0.8 |
0.8 |
0.8 |
90 |
|
0.177 |
0.25 |
3.4 |
1.6 |
1.7 |
1.7 |
1.69 |
80 |
|
0.28 |
0.40 |
5.5 |
2.5 |
2.7 |
2.7 |
2.7 |
70 |
|
0.4 |
0.58 |
7.8 |
3.6 |
3.8 |
3.9 |
3.9 |
60 |
|
0.55 |
0.8 |
10.6 |
4.95 |
5.2 |
5.3 |
5.25 |
50 |
|
0.73 |
1.04 |
14.05 |
6.5 |
6.9 |
7.05 |
6.9 |
40 |
|
0.95 |
1.37 |
18.5 |
8.6 |
9.05 |
9.3 |
9.12 |
30 |
|
1.33 |
1.83 |
24.7 |
11.5 |
12.10 |
12.4 |
12.19 |
20 |
|
1.83 |
2.61 |
35.3 |
16.4 |
17.3 |
17.7 |
17.44 |
10 |
|
2.4 |
3.4 |
45.9 |
21.4 |
22.5 |
23.04 |
22.7 |
5 |
|
2.8 |
4.0 |
54 |
25 |
26.4 |
26.9 |
26.6 |
3 |
|
3.65 |
5.23 |
70.6 |
32.9 |
34.6 |
35.4 |
34.9 |
1 |
|
4.2 |
6.02 |
81.3 |
37.8 |
39.8 |
40.75 |
34.9 |
0.5 |
|
5.48 |
7.85 |
105.9 |
49.3 |
51.9 |
53.14 |
52.33 |
0.1 |
It
can be seen from table4 that the required thickness of each material at any incident
photon energy can be calculated and estimated. It can also be seen that most of
these materials need a greater thickness and the reason for this is due to
their low and close densities in relation to the other materials used such as
lead and tungsten.
It can be stated that the use of radioactive materials, naturally or artificially in the fields of health, education, and other desplines has become relatively easy, after taking into account all the necessary precautions to avoid all the harmful effects of the products of nuclear radiation. Therefore, biological shielding materials can be chosen on the bases of efficiently absorb hazard radiation. It is clear that the best of these materials is lead since it is very heavy element (Z = 82) and it has a widespread use as a biological shielding material. It can be said that materials that contain a large number of electrons per unit volume are necessarily among the best absorbers for gamma rays.
6. Conclusion
Radiation played an effective role in the unique advances in research and science. At low photon energies in the keV range, there are three basic interactions that take place with matter. These interactions are the phenomenon of photoelectric absorption, Compton scattering, and Rayleigh scattering. The study of the interaction of photons with matter at low energies showed enormous potential for medical applications of x rays in non-destructive imaging techniques. This study led to the conclusion that it is possible to photograph any substance or obtain shades of this substance without destroying it in order to identify its components, atomic properties (z atomic number) and its physical properties (electronic density). A deeper understanding of these interactions has developed many spectroscopic techniques and their applications to research, industry, and different medical desplines. Understanding the mechanism of these interactions, coupled with knowledge of atomic systems, make available much of the basis for the theory and practice for radiation health hazard protection and protection around radiation sources. However, due to fact that ionizing radiation can damage biological systems; all countries have enacted severe laws to control exposures of the public and workers to radiation. Today, many unparalleled and wonderful benefits for human life, as well as in scientific and medical research and in industry, that are recognized through the application of different radiation sources, with an emphasis on protecting workers and the public from radiation and its sources.
References
[1] W. Heitler, (1955), “Quantum Theory of Radiation”, Sec. 26, Oxford
[2] R. D. Evans, (1955), ‘The atomic nucleus’ , McGraw Hill Book Company, Inc., New York.
[3] C. M. Davisson and R. D. Evans, (1952), ‘Gamma-ray absorption coefficient’. Rev. Mod. Phys, V24,79-103.
[4] Harvey Hall, (1936), ‘The theory of photoelectric absorption for x-rays and Gamma-rays’, Reviews of modern physics, Vol 8, pp358-377.
[5] J. Hubbel , (1982), ‘Photon mass Attenuation and Energy-Absorption Coefficients from 1keV to 20keV, Int. J. appl. radiat. isot, .vol 33 ,1269-1290.
[6] National Bureau of Standarads,(1969), “Photon Cross Sections, Attenuation Coefficient, and Energy Absorption Coefficients From 10 keV to 100 GeV”, U.S. Department of Commerce.
[7] Compton, A. H., (1923), “A Quantum Theory of the Scattering of X-rays by Light Elements”, Phys. Rev., 21, 483
[8] Compton, A. H., (1923), “The Spectrum of Scattered X-Rays”, Phys. Rev., 22, 409
[9] Cooper, M. J., (1985), “Compton scattering and electron momentum determination”, Rep. Prog. Phys., 48,415
[10] Williams, B., (editor) (1977), “Compton Scattering”., New York: McGraw-Hill.
[11] S. A. Hamouda., (2017)., “Compton Scattering: A Theory and Experiments’, International Journal of Geology and Environmental Sciences., Volume – 5 Issue – 4 August.
[12] S. A. Hamouda; (2016), “Gamma-Ray Compton Spectroscopy of Tungsten Using 662 KeV Gamma-Ray Radiation”, Journal Mordovia University Bulletin. Vol. 26, no. 2, 211
[13] S. A. Hamouda., “The influence of the Detector Response Function of Gamma-Ray Spectrometer on the asymmetry of Compton Profiles”. AL – NAWAH ,Scientific Magazine Issued by Nuclear Research Center. Tripoli- Libya Vol 7 / No. 11 (2008)66 [14] S. A. Hamouda., (2010), “Geometrical and Source Broadening Corrections for High Gamma-Ray Compton Spectrometer” AL – NAWAH, Scientific Magazine Issued by Nuclear Research Center. Tripoli- Libya, Vol. 9 / No 13, 48