Fundamentals and Practices of Sensing Technologies

by Dr. Keiji Taniguchi, Hon. Professor of Engineering

University of Fukui, Fukui, Japan

Xi’ an University of Technology, Xi’ an, China

Dr. Masahiro Ueda, Professor of Faculty of Education and Regional Studies

 University of Fukui, Fukui, Japan

Dr. Ningfeng Zeng, an Engineer of Sysmex Corporation

(A Global Medical Instrument Corporation), Kobe, Japan

Dr. Kazuhiko Ishikawa, Assistant Professor

Faculty of Education and Regional Studies, University of Fukui, Fukui, Japan

 

[Editor’s Note: This paper is presented as Part IV of a series from the new book “Fundamentals and Practices of Sensing Technologies”; subsequent chapters will be featured in upcoming issues of this Journal.]

 

 

Chapter 2: Overviews of Classical Transducers

 

Summary

In this chapter, we provide an overview of several physical transducers and sensors

including analog signal processing circuits. The descriptions that we provide are as

follows : in section 2.1, thermocouple temperature transducers; in section 2.2,

transducers using changes in electrical resistance; in section 2.3, transducers using

 differential transformers; in section 2.4, capacitive transducers; in section 2.5, PZT

 transducers; in section 2.6, optical sensors using photo devices; in section 2.7,

analog signal processing circuits; and in section 2.8, application examples for

 measurements.

 

2.1 Thermocouple Temperature Transducers

2.1.1 Electrical Characteristics of Thermocouples

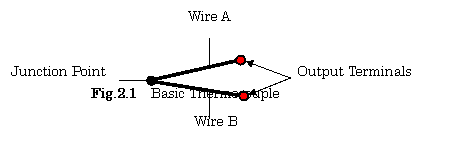
Thermocouples are widely used as temperature transducers. As shown in Fig.2.1, an output signal is generated between the terminals of two dissimilar junction conductors (wire-pairs) A and B, which were made by contacting and welding the two conductors together, when the junction point of a thermocouple has a temperature difference for a reference point. This phenomenon is well known as the Seebeck- effect. Therefore, this transducer is a temperature -to-EMF (electro-motive-force) converter which can produce an output voltage without any additional power sources.

 

 

 

 

 

 

 

Various dissimilar metal combinations are utilized for this transducer, and most frequently used combinations and their output characteristics, i.e., the relationship between the output signals and temperature based on difference from the ice point are shown in Fig.2.2. In this figure, symbols Fe, CR, AL, Pt, Rh, W, CN, and Cu express an ion, a chromel, an alumel, a platinum, a rhogium, a tungsten, a constantan, and a copper, respectively. The output voltage-rate of an iron- constantan, and an chromel- alumel themocouples are about , and, respectively, as shown in this figure.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

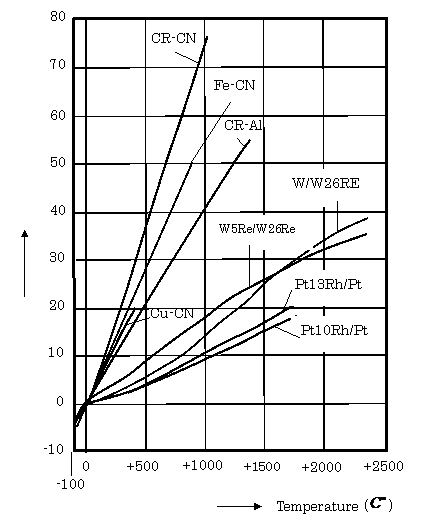
Fig .2.2　Relationships between Temperature and Output Voltage of Thermocouples This figure was reprinted from Fig.13.20 in Ref. (1)

 

 

 

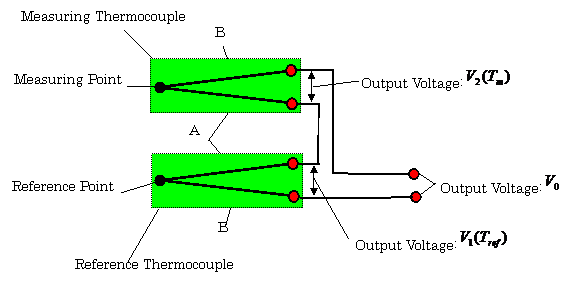
2.1.2 Extension of Output Terminals

In the extension of the output terminals as shown in Fig.2.3, a pair of copper twisted  wires is used for reducing noise induced in the extension wires. In this case, the thermal EMF at junction points 2 and 3 have canceled each other (See Fig.2.5). As a result, a thermal EMF at junction point-1 is obtained from the output terminals of this sensor.

 

 

 

 

 

 

 

 

 

 

 

2.1.3 Differential Thermocouples

As shown in Fig.2.4, the differential connections of thermocouples are used for measuring the temperature difference between two points, i.e., one is the measuring point (measurand), and the other is a reference point. In this case, the output voltage

of the differential thermocouples is expressed as follows: 

 

where  is the temperature of the measuring point,  is the temperature of the reference point, is the output voltage of the reference thermocouple, and is the output voltage of the measuring thermocouple.

 

 

 

 

.

 

 

 

 

 

 

 

 

	Fig.2.4 Differential Thermocouples

 

 

 

This method is available for both surface contact and immersion applications.

 

【Example 2.1】Find the algebraic summation of the thermocouple’s EMF in a circuit composed of dissimilar wires A, B and C as shown in Fig.2.5, where A,B and C express the thermocouple wires and copper wires, respectively. Numbers 1,2,3,4,5 and 6 also express junction points in this figure, ,  and  express the measuring temperature, the reference temperature and the room temperature, respectively. and , , and ,() express the output voltages of the junction points 1,2 and3,4,5,6, respectively.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

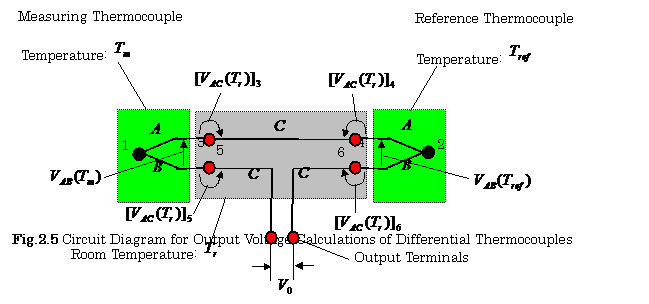
【Solution】

(1) From Fig.2.5, the output voltage is expressed as follows:

(2) The thermal EMF at junction points 3,4,5 and 6 have the same values. Therefore,

(3) From the results mentioned above, we can obtain the following result:

 

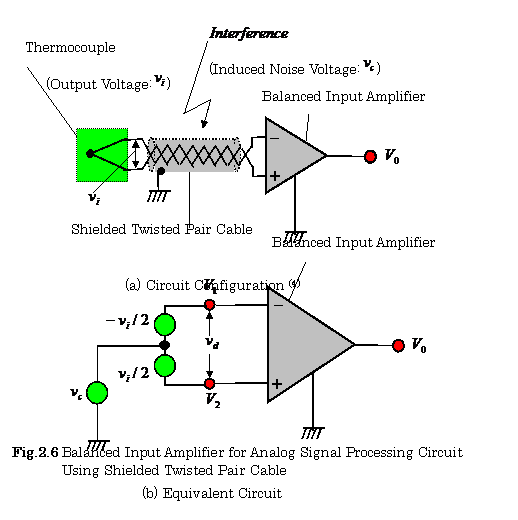
2.1.4 Analog Signal Processing Circuit for Thermocouple Transducers

Figure 2.6 shows a balanced amplifier for an analog signal processing circuit using a shielded twisted cable for the thermocouple transducer. In this figure, (a) and (b) show a circuit configuration and its equivalent circuit, respectively, where signals  and express the output voltage of a thermocouple and an induced noise voltage in the shielded twisted pair cable, respectively.

The use of a shielded twisted cable can reduce the interference due to inductive　and capacitive noise pickup. The details of this circuit are described in section 2.7 of this chapter.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.2   Transducers Using Change of Electrical Resistance

2.2.1 Introduction

As well known, the resistance of a conductor is expressed as follows:

     (2.1)

where is  the uniform cross sectional area of the conductor,  is the length of the conductor, and   is the resistivity of the conductor. In transducers using the change of electrical resistance, the lengthand the cross sectional area are expressed as a function of  force or pressure (force/unit area), and the resistivity is also expressed as a function of  temperature or  force.

 

2.2.2   Temperature - Sensing Transducers

A. Solid Metals or Wires Resistive Temperature Transducers

A resistivity of highly conductive solid metals or wires increases with a change in temperature. The resistivity of a conductor at the temperature is expressed as follows from Matthiessen’s law:

  (2.2)

where  is the resistivity of the conductor at the reference temperature ,

is the temperature coefficient of resistivity at , is the temperature difference: .

The resistance of  Eq. (2.1) is, then, rewritten as follows:

 

where .

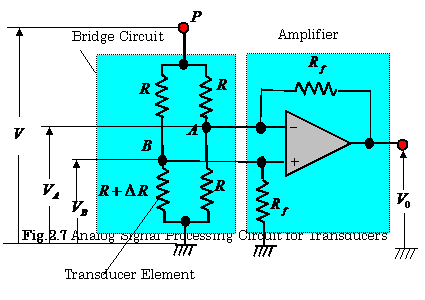
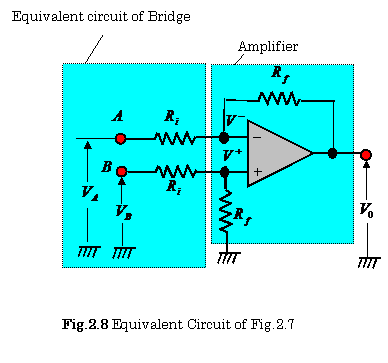
Figure 2.7 shows an analog signal processing circuit for these transducers. The output voltage of this circuit is expressed as follows:

    (2. 4)

 

 

 

 

 

 

 

 

 

 

 

 

 

The platinum, copper and tungsten wires were usually used as the conductors for thermocouples. The ranges of temperature difference are approximately from -180℃ to +630℃.

【Example 2.2】Find the output voltage in the circuit shown in Fig. 2.7.

(Solution)

Let’s analyze as follows using the Thèvenin theorem:

(1)    We have to cut the two input lines of this amplifier and have to open these input lines . As a result,  the voltages  and shown in Fig.2.7 are expressed as follows:

  ,

(2) The resistance between A and B is expressed as, when both points between the terminal P and the ground of the bridge circuit are connected.

(3) Figure 2.8 shows an equivalent circuit of Fig.2.7, which can be obtained by means of Thèvenin theorem. The following equations are obtained from this figure:

　,  , 

The output voltage of this amplifier is, then expressed as follows by means of theses equations:

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B. Semiconductor Resistive Temperature Transducer

Thermistors with resistances of NTC (negative temperature coefficient) are ceramic semiconductors. The NTC thermistors change their resistance exponentially with a change in temperature. These thermisters can, then, be used as temperature

transducers.

The resistance at the temperature of the thermisters is expressed as follows:

     (2.5)

where  is the resistance at the temperature , is the thermister coefficient.

【Example 2.3】In a thermistor temperature sensor , find a thermistor constant, when  and  are  the  resistance values

  in temperatures and  ,respectively.

(Solution)

From Eq. (2.5),  and  are expressed as follows:

_,.

From these equations, the thermistor constantis expressed as follows:

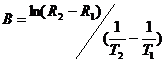_(2.6)

 

Thus, the relationship between the resistance and the temperature is expressed as a non- linear characteristic. From Eq. (2.5), a small change in the resistance R can be approximated as follows:

             (2.7)

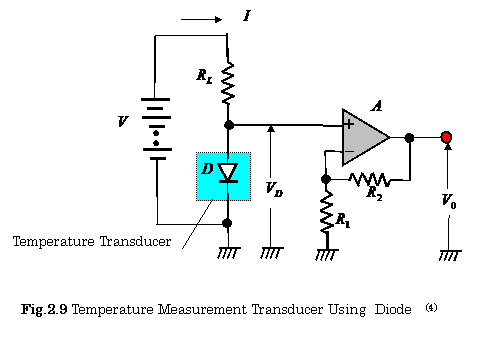
C. Temperature Transducers Using Semiconductor Devices

Forward-biased semiconductor devices can be used for temperature measurements.   Figure 2.9 shows a circuit for temperature transducers. A p-n junction diode is used for these purposes.

 The Relationship between the voltage change and the temperature change is expressed as follows (See comment 2.1):

  ()       (2.8)

In this circuit, the current  has to be a constant-amplitude. This transducer can measure a temperature within the error of 0.1 ℃　over a range of approximately .

 

 

 

 

 

 

 

 

 

 

 

 

 

【Comment 2.1】The -   characteristic of a p-n junction diode is expressed by the following basic equations⁽¹⁰⁾:

,, ,

where is a constant, is the absolute temperature,  is the Bolzmann constant,is the electron charge, and  is the energy gap.

The following equation can be easily obtained from above equations:

    (1)

where , ,,,

.

 From Eq.(1) and the constant values , we can find the following relations:

,,

  ,      (2)

【Example 2.4】In the design of  the sensor shown in Fig2.9 , show a necessary condition for which the current  can be operated as a constant-amplitude.

(Solution)

From Fig.2.9, the current is expressed as .  The necessary condition for which is the constant- current, is as follows:

　　（）　         (2. 9)　

 

2.2.3 Strain Gage Transducers Using Solid Metals or Semiconductors

Strain gages are electromechanical transducers which convert a change in strain into a change of electrical resistance.

Strain gage transducers are used for measuring a force, a pressure, and a flow.

Strain gages are made of solid metals or semiconductors. Figure 2. 10 shows the square bar which constitutes an electrical conductor. In this figure, one end of this bar is fixed, and the other end is stretched with the force.

The average strain is defined as follows:

           (2.10)

where  is the original length,  is the change in length.

The sensitivity of the strain gage is defined as follows:

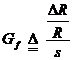          (2.11)

where is the original resistance .  is the change in resistance.

The values of  are approximately from 40 to 200.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

【Example 2.5】In the case that the cross-section of conductor shown in Fig.2.10 has a circular one, the parameters are given as: ,,,,  and .

Find the change of resistance.  where  is the diameter of the conductor .

(Solution)  A cross-sectional area:

           　　.

We can, then obtain the following results from Eqs.(2.10)  and(2.11).

  　　

 

【Example 2.6】⁽⁹⁾

When a tensile force acts on the conductor shown in Fig. 2.10, the length and the cross-sectional area of the conductor will be  and , respectively. Show the following relation:

　　　　(2.12)

whereand   are the Poisson’s　ratio and the change of resistivity, respectively.

(Solution)           

The change of resistance can be expressed as follows as a linear approximation:

　　　　　（１）

_where    

　 ,　　　　　,　 　　　,　　,

_,　Poisson’s ratio:　

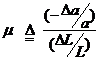
From the above equations, we can, then, obtain a following relation:

_（２）

 

 

2.3 Transducers Using Differential Transformers

2.3.1 Configuration of Linear Variable Differential Transformer

Figure 2.11 shows a displacement transducer using a linear variable differential transformer (LVDT).　This device consists of a ferrite core, a primary coil A, secondary coils B and C.  The secondary coils are differentially connected in each other.  is a voltage source applied to the primary coil, where a frequency  has to be greater than the upper limit of the transducer frequency response.

 

 

 

 

 

 

 

 

 

 

 

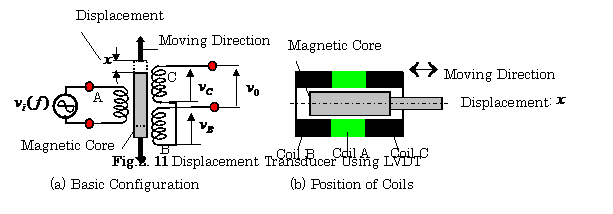
2.3.2   Output Voltage Characteristic of LVDT

In Fig.211, the output voltage of the LVDT is expressed as follows:

          (2.13)

where  is the displacement,  is a constant which depends on the structure of the transducer. Thus  increases linearly for the increase of  

 

2.3.3 Circuit for Obtaining DC Output from LVDT

The output voltage of the LVDT is the AC voltage. A linear rectifier circuit shown in Fig.2.12, is, then, used to convertinto DC voltage　.

 

 

 

 

 

 

 

 

 

 

The linear rectifier circuit consists of small signal linear rectifier circuits and a subtracting amplifier.

Figure 2.13 shows a block-diagram of a small signal linear rectifier circuit.

【Example 2.7】Find which is shown in Fig.2.13 .

In this figure, the small signal linear rectifier circuit and a subtracting amplifier are shown in Fig. 2.36 and Fig. 2.34, respectively.

【Solution】The following result is obtained from Eqs.(2.29) and (2.31).

 ,

 

 

 

 

 

 

 

 

2.3.4   Example of Force Sensor

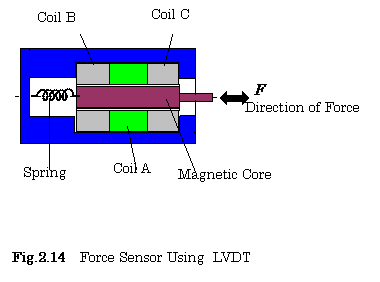
Figure 2.14 shows a force sensor using the LVDT. The force is converted into the displacement using a mechanical spring as follows:

　　　　(2.14)　

where  is the force which acts on the LVDT,  and is a spring constant.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.4    Capacitive Transducers

2.4.1 Introduction

As well known, the capacitance between electrodes, A and B shown in Fig.2.15 is expressed as follows,

　　　　　(2.15)

where is the area of a electrode, , is the gap distance between electrodes, , is a relative permitivity.

 

 

 

 

 

 

 

A transducer using electrical capacitance, can thus be expressed as a function of the area of an electrode, the gap distance between electrodes, and the relative permitivity of a substance between electrodes A and B (See problem 2.1).

 

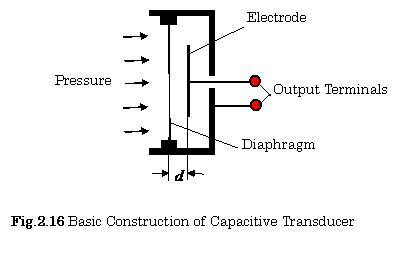
2.4.2 Capacitive Transducer Using Gap Distance

Figure 2.16 shows a basic construction of a capacitive transducer using the gap distance . The small change in the capacitance due to the small change in the gap distance is expressed as follows:

A typical transducer of such a structure is a condenser microphone.

 

 

 

 

 

 

 

 

 

【Example 2.8】Derive Eq.(2.16)

【Solution】From Eq.(2.15), the following result is obtained.

 

2.4.3   Capacitive Transducer Using Area of Electrodes ⁽⁵⁾

A. Basic Circuit Configuration

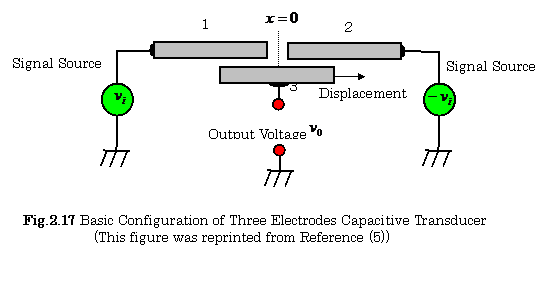
Figure 2.17 shows a capacitance transducer using three electrodes, where electrode 3 is moved to the right direction with a distance.

The capacitance  between electrode 1 and electrode 3 　decreases linearly with  , while the capacitance  increases linearly with .

 

 

 

 

 

 

 

 

 

The voltage  between electrode 3 and the ground is expressed as follows:

　　　(2.17)　

where  is the voltage between electrode 1 and the ground, and  is the voltage between electrode 2 and the ground.

is the capacitance between electrodes 1 and 3, and  is the capacitance between the electrodes 2 and 3.　　　　　

The value of  in Eq.(2.17) can be approximated as a constant, when the

maximum range of the displacement is between  and as shown in Fig.2.18.

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 2.19 illustrates the fringe effect between electrode 1 and the left edge of electrode 3. In this situation, the value of  is not constant. Therefore, the relationship between the output voltage and the displacement  is non-linear characteristic.

 

 

 

 

 

 

 

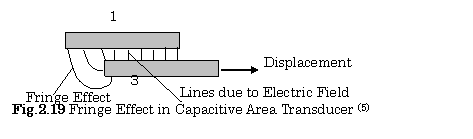
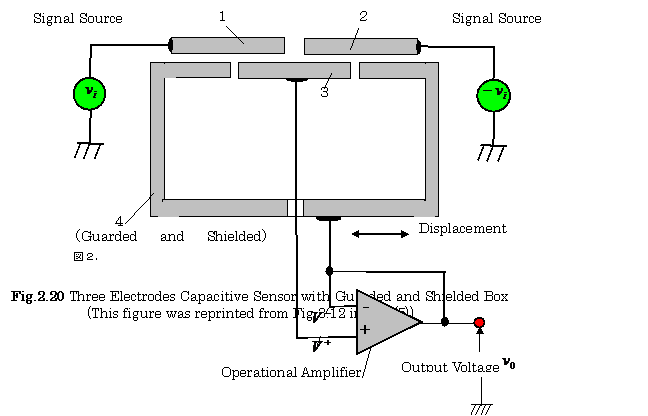
B．Practical Configuration

For minimizing the fringe effect, a guarded and shielded box is used as shown in

Fig.2.20, where an input voltage  of an operational amplifier nearly equals to the other input voltage  of that.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

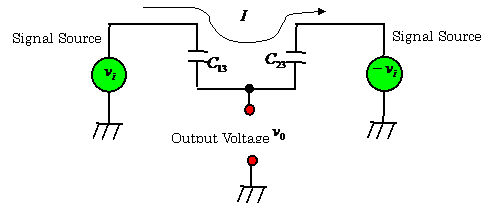
【Example 2.9】Derive Eq. (2.17).

【Solution】The following equations are obtained by means of an equivalent circuit shown in Fig. 2.21.

　,　　　　

From these equations, the following result is obtained.

　　　

 

 

 

 

 

 

 

 

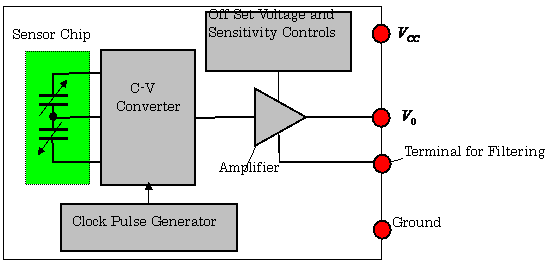
C．Example of Capacitive Sensor ⁽⁶⁾

Figure 2.22 shows an example of an acceleration sensor device using a capacitive sensor chip. The sensor chip in this figure is made of an ASIC technology.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.5 PZT Transducers^{(1), (2)}

2.5.1 Introduction

PZT ceramics are mainly used as piezoelectric materials. The root of the word “piezo” means pressure, and thus, piezoelectric material implies pressure electric one.

Chemical components of PZT ceramics are , where chemical symbols  Pb,  ,  and  express  lead,  zirconate,  titanate, and oxygen, respectively.

 

2.5.2 Mechanical and Electrical Characteristics of PZT

 PZT that has elastic characteristics, convert mechanical stress into electrical polarization and vice versa.

Figure 2.23 (a) shows the relationship between the stress (force per unit area) which acts on the PZT, the resulting electrical polarization (electrical charges) , caused on the PZT.

(1) When the mechanical stress  is given to the PZT, it produces the polarization .

The relationship between the two is expressed as follows:　

where  is the piezoelectric constant. This phenomenon is called the piezoelectric effect.

(2) In contrast, when the electric field  is given to the PZT as shown in Fig. 2.23(b), it produces the mechanical distortion .

The relationship between the two is expressed as follows:　,

where is the piezoelectric constant. This phenomenon is called the reverse piezoelectric effect.

(3) As described above, the PZT is the elastic material. So, The relationship between the stress and the strain  is expressed as: ,

where  is the compliance.

(4) The PZT is the dielectric material. So, The relationship between the electric displacement  and the electric field  is expressed as: ,

where  is the dielectric constant.

From the relations mentioned above, the mechanical distortion  and the electric displacement  and described by the linear equations:

 

       (2. 18)

       (2.19)     

 

where , and  are tensors,and  are column vectors.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

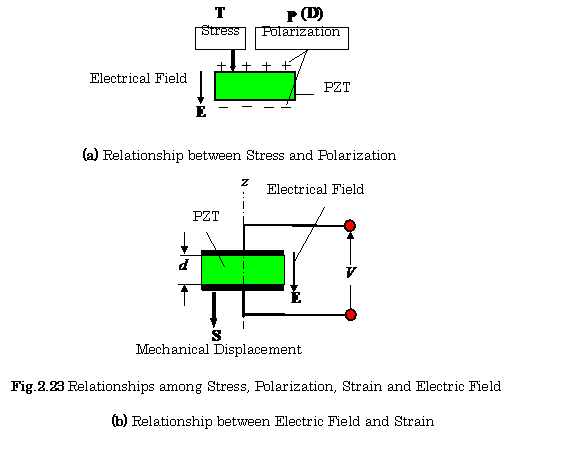
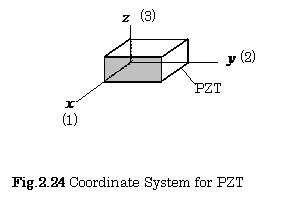
Figure　2.24 shows the coordinate system for the PZT ceramics, and the numbering expressions. Where, subscriptions 1,2, and 3 express the x, y, and z- axes, respectively.

Table 5.1 shows these relations.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1          　6          5                    2          4                                         3

Table 5.1 Subscriptions used here

 

 

 

 

 

 

 

 

 

 

As an example described above, we show the stress-strain relations as follows:

 

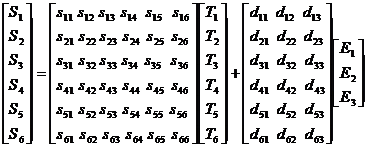    (2.20)

 

【example 2.10】

In Fig.2.23　(b),  when the stress is zero(), determine the following values:

(1) strain ,

(2) displacement .

【Solution】From Eq.(2.18),and Fig.2.23, we obtain the following results.

,  ,  ,

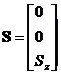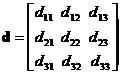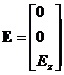(1),   (2)From ,  , and ,

 is expressed as:.

 

【Example 2.11】From Eq.(2.20), the mechanical distortion  and the electric displacement  for the longitudinal vibration of the rectangular ceramic element shown in Fig.2.25 are described by the following equations:

 

 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.5.3 Pyroelectricity

The electric polarization in the PZT is also caused by thermal expansion. Such an effect is called pyroelectricity. The pyroelectric coefficient  is defined as the partial derivative of the displacement with respect to the temperature  at constant electric field , and it is expressed as follows:

     (2.21)

2.5.4 Applications

The details of these applications are described in almost all the sections throughout in chapter 3.

 

[Part II of Chapter 2 will be presented in the upcoming November-December 2009 issue of this Journal.]