Globalization: World Population:

Mathematical Descriptions of Population Trends

by Dr. Julio A. Gonzalo¹ and Dr. Manuel Alfonseca²

¹ Escuela Politécnica Superior, Universidad San Pablo CEU, Montepríncipe, Bohadilla del Monte, 28668 Madrid, Spain. Departamento de Física de Materiales, Universidad Autónoma de Madrid, 28049, Madrid, Spain, e-mail: julio.gonzalo@uam.es

² Escuela Politécnica Superior, Universidad Autónoma de Madrid, Francisco Tomás y Valiente, 11. 28049, Madrid, Spain, e-mail: manuel.alfonseca@uam.es

Abstract

Mathematical models of demography and population trends have been with us since two and a half centuries ago. As the subject matter is extremely controversial, experts frequently disagree. In this paper we have selected six of the main milestones in this field, which we have completed with a short description of our own work in the area.

Introduction

In this paper we have selected six of the main milestones in the field of population dynamics, namely: Edmond Halley, Leonhard Euler, Thomas Robert Malthus, Pierre François Verhulst, the Club of Rome and Robert McCredie May, following mainly a recent historical book (Bakaër 2011), which we have completed with a short description of our own work in the area.

Edmond Halley (1656-1742)

Around 1690, Caspar Neumann collected data in Breslau (Wroclaw) about the number of births and deaths in his city and the age of people at death. Neumann sent his data to Henry Justel (secretary of the Royal Society). Halley got hold of the data, analyzed them, noticed that the population, the number of births and the number of deaths remained constant in those  five years (1687-1691) and built a life table showing the population in the city as a function of age. His formula was simple: given that P₀ = population with 0 years of age must be equal to the number of births in the year (a mean of 1238), the population at age k+1 must be:

(1)

where D_k is the number of deaths in the year at age k. Adding all the elements in the table, Halley got an estimate of the total population of Breslau (which had not been stated in Neumann’s data) as about 34,000. Halley then used the data to build a table to compute the price of life annuities, although his results (which were reasonable) were never taken into account in practice. This table was built starting from the fact that the probability that a person who is alive at age k be still alive at age k+n would be , which could be computed from his life table.

Leonhard Euler (1707-1783)

The famous Swiss mathematician Euler was also one of the pioneers of mathematical demography. Rather than tackling a stable population, as Halley had done, Euler considered the situation where a population grows at a constant rate x. As the situation is exactly the same as that in compound interest, the formula he reached was:

(2)

where P₀ is the initial population and n is the number of years. This formula corresponds to a geometric progression, also called an exponential growth.

In a later work (A general investigation into the mortality and multiplication of the human species), published in 1760 in the Proceedings of the Academy of Sciences in Berlin, he analyzed the following situation:

·       A population in exponential growth: 

·       The birth rate is constant: m = B_n / P_n. Therefore .

·       The death rate is constant, ergo . From here we get: . Also, .

·       Let P_k,n be the population at the beginning of year n with an age k. The survival coefficient q_k (the proportion of the population that reach age k) is: q_k = P_k,n / P_0,n-k. These coefficients can also be computed thus: , where D_k,n is the number of deaths at age k during the year n. The initial coefficient is q₀ = 1.

·       The maximum age reached by a member of the population is 100 years.

From these assumptions, Euler derived his demographic equation, namely:

(3)

which is the same as Halley’s equation when r=1.

Although Euler was the first to prove that in a population in exponential growth the shape of the age pyramid remains constant, this discovery was not taken into account until it was rediscovered in the twentieth century. Of course, assuming an exponential growth for extended periods would be an unrealistic assumption.

Thomas Robert Malthus (1766-1834)

In 1798, Malthus published (anonymously) a book entitled An essay on the principle of population, as it affects the future improvement of society, with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers. This book includes the famous quotation:

Assuming then my postulata as granted, I say, that the power of population is indefinitely greater than the power in the earth to produce subsistence for man.

Population, when unchecked, increases in a geometrical ratio. Subsistence increases only in an arithmetical ratio. A slight acquaintance with numbers will skew the immensity of the first power in comparison of the second.

In other words, population grows exponentially (or in a geometric progression) as Euler had assumed, but food production grows in an arithmetic progression, i.e. linearly. Therefore, the geometric increase of the population must be stopped by the effects of famine.

Malthus made two mistakes:

1.     Extending the exponential growth of population indefinitely. As Gordon Moore expressed it in a meeting of the IBM Academy in 2003: No exponential is forever.

2.     Assuming that food production cannot grow exponentially. However, the agricultural revolution of the nineteenth and twentieth century produced exactly that result.

Charles Darwin and Alfred Russell Wallace applied (and cited) the ideas of Malthus to develop the theory of evolution by means of natural selection.

Pierre François Verhulst (1804-1849)

In 1838, as a reaction against Malthus theory, the Belgian Verhulst proposed (in his Note on the law of population growth) the following equation to represent the growth of population:

(4)

This is the logistic equation. Parameter K is arbitrary. If its value is infinite, we get exponential growth. If it is finite, the solution to this equation resembles exponential growth up to an inflection point (at a value of P=K/2) and then becomes convex upwards and grows ever more slowly until it reaches (at time infinite) the value K. Figure 1 shows the logistic curve.

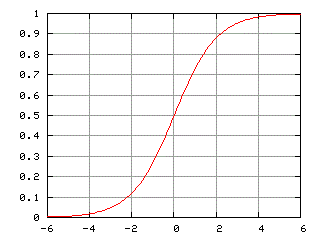
Figure 1. The logistic curve for K=1.

Verhulst tested the logistic curve against real data from France, Belgium and the U.S.A.  and got a good fit. However, his predictions for longer times (around 50 years) did not come true. The problem in his case is that the two parameters in his equation (the growth rate r and the limiting value K) are not really constant, but time dependent. With an appropriate technology that increases the resources of the world along time, the value of K can be increased above its value around the mid-nineteenth century.

Club of Rome (1968-)

In 1972, the Club of Rome published its first report, the best-selling book The limits to growth, which described a model based on five variables: world population, pollution, industrialization, food production and resources depletion. Following Malthus, these five variables are assumed to grow exponentially, while the resource growth as a consequence of technological advances was supposed to be only linear. The model consisted of about 1000 equations, and the authors studied three different future scenarios, two of which would lead to the collapse of human civilization, while the third (of course, favored) would lead to stabilization. The book has been considered too pessimistic and its growth assumptions arbitrary. In fact, world population growth has been observed to go through the inflection point in the logistic curve around 1985, which means that this growth is no longer exponential.

In 1974, the second report of the Club of Rome (Mankind at the turning point) presented a more complicated model (about 200,000 equations), integrating, not just technological, but also social data, which lead to more optimistic predictions, signaling that many of the future factors are under the control of mankind and therefore may be changed.

The reports of the Club of Rome have been checked with real data in the forty years passed since their publication, the reviewers sorting themselves among those who assert that the predictions of the Club are being confirmed, and those who claim that they have been proved incorrect.

Robert McCredie May (1936-)

In 1974, the Australian born Robert May published in Science an important paper addressing the problem of computing the population dynamics when the resources of the environment are limited (in other words, when the population size cannot go much higher than a certain maximum K). The model he proposed was a discrete equivalent of Verhulst logistic equation:

(5)

This equation works for 0<a≤3. Figure 2 shows the solutions for the equation for several values of parameter a, and for K=1000.

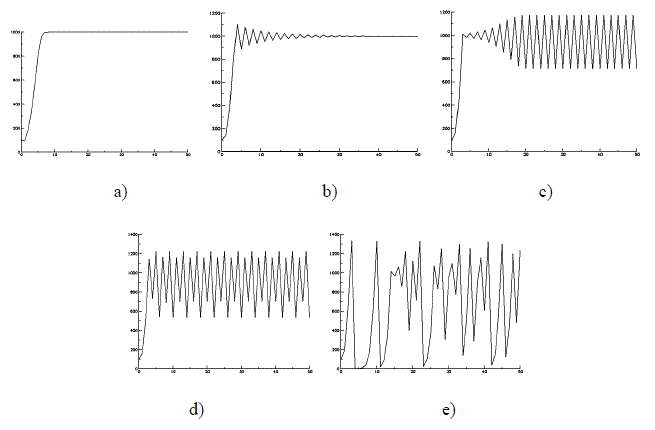
Figure 2. Solutions for May equation. a) a=1; b) a=1.9; c) a=2.25; d) a=2.5; e) a=3.

It can be seen (and proved mathematically) that for a<2, the equation converges to a single value; for 2≤a<2.45, it converges to a period 2 cycle; for 2.45≤a<2.545, it converges to a period 4 cycle; and for 2.57≤a≤3, the equation becomes chaotic. Populations, therefore, can be subject to quite unpredictable dynamics, which makes it possible that the optimistic or pessimistic predictions by different authors may not be according to reality.

Equation (5) can be simplified to (6) by means of the following variable changes:

                             

(6)

Julio A. Gonzalo et al

Using UN population data for the interval 1900-2010, we have simulated its time evolution by means of rate equations inspired on condensed matter physics (Gonzalo et al 2012). The final differential equation to be solved was:

(7)

whose solution is:

(8)

 

where t^* = t / cosh a.

           

Equation (8) describes a step up in population due to an increase in fertility rate, a decrease in death rate (life expectancy increase) or a combination of both, resulting in a net growth rate. This equation fits the UN data satisfactorily and shows clearly that the population increase in 1950–2010 should be attributed more to the transient decrease in death rate level (related to the increase in life expectancy) than to a non-existent increase in birth rate, which was decreasing consistently already even before the 1950s, even before chemical contraceptives and legalized abortion begun to play any role.

An equivalent approximate form of equation (8) is:

tanh⁡

(9)

Using this equation we analyzed the three future scenarios estimated from the UN data and came to the following conclusions (Gonzalo et al 2015): Today the world is not overpopulated and is unlikely to be so in the foreseeable future. Extrapolating present trends shows that total world population may reach a maximum of 7.74 billion by 2050, and by the end of the current century it may have decreased. Assuming that the smooth natural decrease in birth rate by the mid-seventies had continued all the way down, the estimated population maximum would have reached 8.4 billion by 2065, rather than 7.73 billion by 2050; therefore the policies aimed at lowering the birth rate supported by the UN should be reconsidered. The population rise during this century (1950-2050) is due to the high and sustained decrease in death rate (and the corresponding high increase in life expectation) rather than an increase in fertility that actually never happened.

References

 

1.      Nicolas Bacaër, 2011. A short history of mathematical population dynamics, Springer.

2.      Meadows, D. H.; Meadows, D. L.; Randers, J.; Behrens III, W. W., 1972. The Limits to Growth: a report for the Club of Rome's project on the predicament of mankind, Universe Books.

3.      Mesarovic, M.; Pestel, E., 1974. Mankind at the Turning Point. The Second Report to the Club of Rome, New York: E.P. Dutton.

4.      Gonzalo, J.A., Muñoz, F.F., Santos, D.J., 2012. Using a rate equation approach to model world population trends. Simulation 89(2), 192-198, DOI:10.1177/0037549712463736.

5.      Muñoz, F.F., Gonzalo, J.A., 2013. Falling birth rates and world population decline 1950-2040. Departamento de Análisis Económico, U.A.M.

6.      Gonzalo, J.A., Muñoz, F.F., 2014. Prospects of world population decline in the near future: a short note. Departamento de Análisis Económico, U.A.M.

7. Gonzalo, J.A., Alfonseca, M., 2015. Quantitative estimates of the future world population decline. Journal of Global Issues and Solutions, The Bimonthly Journal of the BWW Society, 6 pp.