The 3-Dimensional Icosahedron Periodic Table

                                                   

By Dr. Chong Soo Han, Department of Chemistry Chonnam National University, Gwangju, Korea

and Dr. Sunah Kim Han, Department of Mathematics, Chosun University

Gwangju, Korea

 

Editor’s Note: Offering a quite interesting mix of science and philosophy, the authors of this paper present a new way of perceiving the Chemical Periodic Table. Whether we hail from the hard sciences, the arts and letters, the humanities or other fields, we have all, at one time or another, encountered the Periodic Table. Presented here is a paper edited for the layperson, giving a new visual  twist to what, prior to now, had always been illustrated in 2-dimension.

 

Since ancient times humans have wanted to transform materials, thus the early refinement of iron, the creation of brass, and so on. In their quest to transform known materials of their era, the ancients conceived the idea of elemental materials, from which a compound material was created. Thus, it was correctly thought, that if such a compound could be physically or chemically divided into its elemental units that the material could be reconstructed into a different compound. The ancients thus strove to identify the elements, and settled on the four elements of soil, water and air and fire.

 

About 350 BC, the Greek philosopher and mathematician, Plato, believed that the universe could be explained from the viewpoint of mathematics and he proposed five elements corresponding to five perfect solids. The perfect solids are the tetrahedron (consisting of four sides, each an equilateral triangle), the cube (six sides, each a perfect square), the octahedron (eight sides, each an equilateral triangle), the dodecahedron (12 sides, each an equilateral pentagon) and the icosahedron (20 sides, each an equilateral triangle).

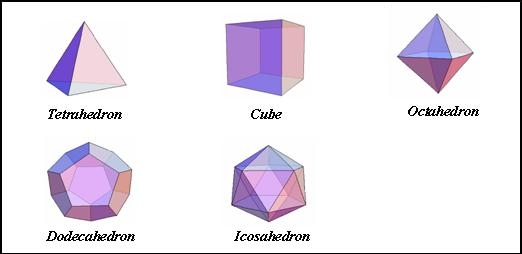
The five perfect solids

Plato equated the tetrahedron to fire, which is currently explained as the plasma state. The cube, the octahedron and the icosahedron were equated to the solid, gas, and liquid phases, respectively. Plato also suggested that the dodecahedron corresponded to an element he called Aether, which he believed could transform the other four elements without changing itself. At times Aether was also referred to as the ‘fifth element’. After the age of the Greeks, alchemists thought that the fifth element was a magical element that could transform the other chemical elements; the alchemists are remembered most famously for their belief that lead could be transformed into gold.  After systemic discovery of a wider and more diverse range of chemical elements, physicists believed a matter, which they called Ether, filled the universe and was the medium through which light was transmitted. In the beginning of the 20th century Einstein proved that ether was not necessary to explain the propagation of light.

 

In the modern era the theoretical ‘fifth element’ is no longer a topic of consideration. However, we know that in previous centuries and previous millennia scientists in both the Eastern and Western cultures believed that five elements explained the universe. As to why this belief in the existence of five elements was predominant -- regardless of place or culture -- in the ancient and pre-Einsteinian eras, it is interesting and perhaps pertinent to note that we also have five fingers, thus perhaps leading to a sort of intuitive belief in the five-element concept. If we consider that perhaps Plato had a transcendental cognition of the elements of the universe, this could be the basis for his theory of the ‘magic’ element Aether, which he believed was dodecahedron-shaped or possibly another perfect solid of a shape which can be placed inside a dodecahedron. Although Plato believed that Aether has characteristics similar to other perfect solids, he had difficulty in describing Aether in relation to the other perfect solids, because at that time the Greeks believed that the water element was sphere-shaped. Thus the icosahedron -- as the solid with a shape most similar to the sphere – was related to water, while fire was related to the edged tetrahedron, soil to the stable cube and air to the unstable octahedron. Plato may have had only a transcendent cognition that Aether might relate to a perfect solid, but without visualized evidence he could not relate it to the solid in opposition to the common belief of the era.

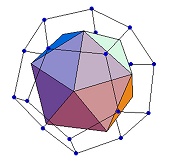An icosahedron in a dodecahedron

 

Following this line of thought -- and taking note of the fact that the dodecahedron has the same symmetry as the icosahedron -- the authors of this paper conceived that, as a mathematician, Plato conceptualized the inside of the dodecahedron mathematically. An icosahedron can be generated from the lines which form the centers of the faces of the dodecahedron (see illustrations, right). A mathematician would say that the dodecahedron and the icosahedron are ‘duals’, as are the octahedron and the cube. Inversely, a dodecahedron can be formed inside an icosahedron with the same method. Similarly, a tetrahedron can be formed inside a larger tetrahedron; this arrangement is referred to as a ‘self dual’. This means there is a possibility that, after recognizing that the supposed ‘fifth element’ corresponded to a solid consisting of 20 faces, Plato conceptualized an icosahedron inside a dodecahedron.

 

In 1871, the Russian chemist Mendeleyev organized the chemical elements known at time into eight families on the periodic table.

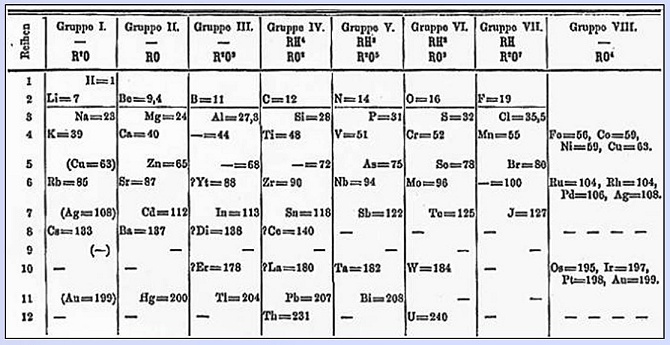
Mendeleyev's periodic table (1871)

 

At present, we know that there are 18 families and two f-block families; correspondingly, we know that the chemical elements can be classified into 20 families, thus relating to the 20-sided icosahedron.

 

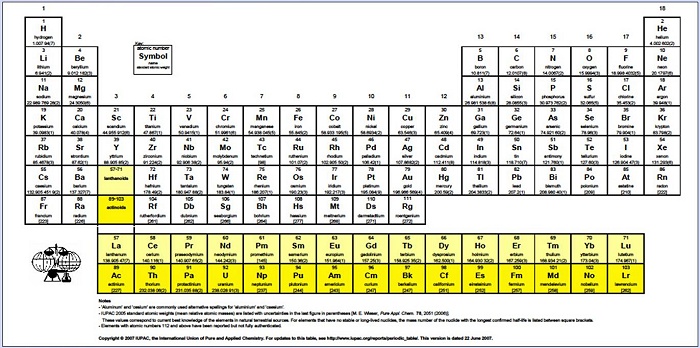
IUPAC periodic table of chemical elements (2007)

If we contemplate two facts, one can find a similarity between the fifth element relating to the 20 faces of the icosahedron and the 20 families of the modern periodic table. In the other words, there is a possibility that, from his transcendental meditation about Aether, Plato may have intuitively known the element has 20 faces. Subsequently, modern chemists found 20 families in the elements from the viewpoint of chemical properties.  

 

Considering the above, we know of the 20 faces in the icosahedron for Aether from the transcendental meditation of Plato, and modern science divides the currently-known elements into 20 families. Conceptualizing what follows requires a jump in one’s thinking. We are parts of the universe and our nature is the same to that of the universe. This means that if one opens one’s mind philosophically, departing from the viewpoints of traditional education and preconceived ideas, one can see the nature of universe. This is the basis of meditation in Buddhism. In the authors’ knowledge, Kant thought about this matter and he mentioned ‘the transcendental knowledge’. Many inspirations of great scientific discovery are achieved in this manner; in fact, Albert Einstein once said that he developed his Theory of Relativity by visualizing himself sitting on a photon as it dashed through space. The authors of this paper posit that Plato (and along with him, Mendeleyev) also had a brilliant clarity of mind, enabling him to visualize the structure of chemical elements. This brings us to a fundamental philosophical question: “Can one find a thing which does not exist in the universe?” Newton said, that in comparison to all that is still unknown to humankind, his discoveries were merely a few pebbles on the seashore. What then, of the entire ocean?

 

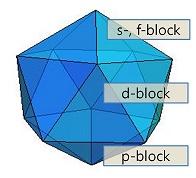The first mapping of an icosahedron and the families of the elements

If there is a relation between the facts, there is a one-to-one mapping between the icosahedron and the periodic table. Interestingly, the icosahedron has 10 faces in the middle band and what are referred to as the ‘d-block transition metals’ can be classified into 10 families. Thus the middle band of the icosahedron directly corresponds to the region of the ten d-block transition metal families, which a chemist would refer to as d¹ through d¹⁰, and would assign them ‘family’ numbers 3 through 12. After this, we can locate five of what chemists refer to as p-block families, p¹ through p⁵, with family numbers 13 through 17 corresponding to the bottom faces of the icosahedron. Then we can assign the last p-Block family, p⁶, family number 18 (which was called the 0^th family for a time) to the top side. After that, two s-block families, s¹ and s², can be arranged in turn. The last two faces of the top side of the icosahedron correspond to the two f-block families, Lanthanide and Actinide. In summary, the 18^th, 1^st, 2^nd, Lanthanide and Actinide families can be located around the faces of the top side of the icosahedron. Then, moving down, we place the 3^rd to 12^th families around the middle band. After filling the middle band, we can position the 13^th to 17^th families along the bottom sides. Thus we have finished the construction of a 3-D icosahedron periodic table via the method of mapping the families of the chemical elements and the faces of the icosahedron.

 

A view of the 3-D icosahedron periodic table of the elements (2010)

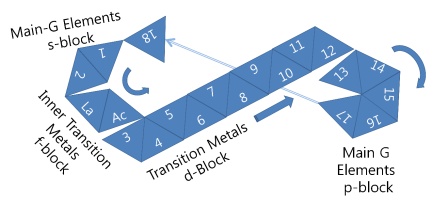A development figure of the icosahedron periodic table of chemical elements

The features of the icosahedron 3-D periodic table are as follows:

1.     We can touch it. This stimulates one’s interest in the elements, relating to chemistry as well as to science in general, from young children taking their first look at chemistry to professional scientists teaching the subject.

2.     In the basic model, the f-block elements are located in their correct position¹.

There are many symmetry operations² in the icosahedron. When one is playing with the 3D periodic table, one’s spatial perception is greatly enhanced.

3.     One can handily rearrange the periodic table depending upon one’s particular interest or experimentation. This is the authors’ proposal for the next generation of chemists, teachers and students. The authors posit that future generations will be able to change the chemical properties of the elements and, correspondingly, they will change the location of the families on the faces of icosahedron. This change, however, does not mean they will be able to change the elements themselves as the Alchemists attempted.

 

In conclusion, the authors of this paper believe that if there are other intellectual living things in the universe, they too will begin their journey of scientific discovery with the recognition of five perfect solids³ and the periodicity of chemical properties⁴ of the elements. We believe they will group the elements into a periodic table as Mendeleyev did. And finally they will make 3-D icosahedron periodic tables to teach science to their children.

 

 

 

Footnotes:

 

1. We should note here that these 14 elements are typically placed outside of the standard two-dimensional periodic table. If we insert them in the 2-D periodic table, the table is too wide. Moreover, the elements Lanthanide or Actinide have similar chemical properties in the groups. They are referred to as inner transition metals. They should be located between s² family (#2) and d¹ family, #3.

 

2. A ‘symmetry operation’ refers to an operation in which an object is of the same shape after the operation as it had prior to that operation. A sphere, for example, has infinite symmetry operations. An icosahedron features five symmetry operations (rotating 360°/5 around the vertices), two symmetry operations (around the center of faces) and two rotations around the center of the edges. It also has five planar reflection operations for the vertices and a point reflection operation for the center. The symmetry operations usually simplify the description of the shapes of objectives. Departing from the material science, we can also apply the concept of symmetry to the numerous sets of two opposing relationships, for example, positive and negative, left and right, good and bad, and so on. The authors believe that a fundamental basis of our cognition is via symmetry operations. In many cases, spoken language -- which expresses our cognition -- has just two symmetry sets and a point in the center, thereby bringing some restriction to understanding nature or society. This may stem from what can be described as 1-dimensional or 2-dimensional education from youth onwards. The 3-dimensional model of the periodic table can enhance one’s spatial perception as well as provide multi-directional view points for understanding the things around us.

 

3. It was proved there can only be five perfect solids in the Euclidian space. It is fairly difficult to understand things in non-Euclidian space and we have no experience in doing so. The authors assumed that Euclidian space is one of the best models for (our) universe at this present time. The point of this paper is generalization of the well-proven things to the whole universe under the belief of the homogeneity of the universe and we are just a part of that.  Einstein also believed and proved that the physical phenomena can be described as the same form for the all observers. It is interesting to note that Mathematics is a strange science; it starts only from a few assumptions but it clearly describes the facts around us. The authors believe that others in the universe also built up mathematics as humans have, step-by-step over time. These others may find points, lines, 3-D solids and five perfect solids as we have done. They can also find that the elements can be classified to 18 families. And, in this far away place, a strange man may correlate the elements and families and posit that the periodicity of the elements can be represented on the faces of icosahedrons in perfect logic(!).

 

4. To explain the word ‘periodicity’ as it is used in this context, we should note that the elements show the chemical properties periodically, as the atomic number of the element increases. Mendeleyev discovered this point. Periodicity is also a basis of our cognition. In modern science, it was believed that the material has wave-particle duality. Since the typical character of the wave is periodicity with space and time, the materials in the universe will show periodicity from the appropriate view points. We also simplified our observation with periodicity, just like symmetry. We express observable things with periodicity. One of the best examples is the measurement of time of in days, our life, the rotation of the earth and so on. We make units based on periodicity, for example, in linear terms, a ruler. In the chemical periodic table, the elements show similar chemical properties periodically as the atomic number of each element increases.

 

This figure below serves as a visual summary of the paper: